II. Zależności statystyczne

Marek Jerzy. Minakowski, Prehistoria logiki formalnej

I. Objaśnienia ważniejszych pojęć

Podstawowym celem niniejszej rozprawy jest przedstawienie pierwocin logiki formalnej; poszukiwanie odpowiedzi na pytanie, czy Arystoteles istotnie był pierwszym logikiem, jaka była znajomość logiki przed powstaniem jego pism logicznych i jak ewentualna logika jego poprzedników miała się do treści Analityk Pierwszych.

Dotychczasowe badania prehistorii logiki formalnej były pobieżne, opinie różnych autorów na jej temat i streszczenie tych nielicznych badań, które przeprowadzono, postaram się przedstawić w rozdziale drugim; tymczasem stwierdzę, że zadaniem, jakie niniejszej pracy zostało postawione, jest przeprowadzenie tych badań od początku. W tym celu zacznę od zdefiniowania podstawowych pojęć, którymi posługuję się w dalszej części rozprawy.

1. Logika

Przez logikę lub logikę formalną będę rozumiał teorię dedukcji, a więc naukę badającą systemy dedukcyjne.

Zaletą takiej definicji jest to, że pozwala ona na rozgraniczenie między tematyką Analityk Pierwszych Arystotelesa, która się w niej mieści, a tematyką Kategorii i Hermeneutyki, która znajduje się w całości poza zakresem definiowanego przez nią pojęcia. Chwyta więc ona — jak się wydaje — intuicje Arystotelesa, które zadecydowały o takim właśnie podziale tej dyscypliny na (m.in.) „hermeneutykę” (teoretycznie opracowaną najpełniej w Hermeneutyce), czyli — ogólnie mówiąc — teorię zdania, i „analitykę” lub „sylogistykę” (teoretycznie opracowaną w Analitykach Pierwszych), a mianowicie dyscyplinę zajmująca się sylogizmami.

„Sylogizm jest to wypowiedź, w której, gdy się coś założy, coś innego, niż się założyło, musi wynikać dlatego, że się założyło”. Będziemy się więc zajmowali wypowiedziami, w których coś z czegoś z konieczności wynika wyłącznie na mocy założeń. Nie będziemy się zajmowali wypowiedziami, w których coś wynika w inny sposób (jak w wynikaniu materialnym, wykorzystującym reguły dowodzenia, które nie są ważne na mocy samej tylko logiki). Nie będziemy się też zajmować wypowiedziami, w których nie ma żadnego wynikania ani implikacji.

Takie rozumienie logiki wyklucza wiele znaczeń przypisywanych słowu „logika” w różnych epokach. Jeżeli, jak to niegdyś robiono, podzielimy logikę na logikę formalną i logikę materialną, to praca niniejsza należy do historii logiki formalnej, nie zajmuje się więc dziedzinami badającymi materialną stronę poznania, zaliczanymi dziś raczej do filozoficznej teorii poznania, psychologii poznawczej, językoznawstwa lub semiotyki.

Gdyby przyjąć używaną czasami dystynkcję na logikę filozoficzną i logikę matematyczną, to przedmiot niniejszej pracy mieści się w historii logiki matematycznej.

Taka definicja logiki pomija też pewne tematy zaliczane do logiki matematycznej czy formalnej dziś. Nie wchodzą do niej wypowiedzi, w których nie pojawia się ani implikacja, ani wynikanie, a w szczególności prawa wyłączonego środka i niesprzeczności. Arystoteles nie zajmował się nimi w swych pracach logicznych, ale w Metafizyce. Jak pokazał Łukasiewicz [1987], ich wersje logiczne należy rozpatrywać razem z wersjami ontologicznymi i psychologicznymi. Przedarystotelesowe losy tych „aksjomatów” powinny być przedmiotem osobnej monografii, podobnie jak stało się to z ich miejscem u Arystotelesa.

Z pewnością Arystoteles mówiąc o tym, że przed nim nie było w tej nauce żadnych badań, nawet wstępnych, nie miał na myśli teorii praw niesprzeczności i wyłączonego środka, chociażby dlatego, że w księdze Γ Metafizyki odwołuje się do poglądów filozofów, którzy się na te tematy wypowiadali.

W pewnych kontekstach pod pojęciem „logika formalna”, lub krócej: „logika”, będę rozumiał nie teorię dedukcji, ale jej przedmiot, a w szczególności system dedukcyjny logiki pierwszego rzędu z teorią mnogości. Nie powinno to jednak prowadzić do nieporozumień, zwłaszcza że kieruję się tu powszechnym zwyczajem.

2. Dowód i pojęcia pokrewne

Przez dowód będę rozumiał wypowiedź w języku naturalnym, którą da się przedstawić w postaci derywacji w jednym z systemów dedukcji naturalnej Gerharda Gentzena, tak jak są one przedstawione np. w artykule Daga Prawitza Ideas and results in proof theory.

Derywację będącą przedstawieniem danego dowodu będę nazywał jego formalizacją.

Założeniem będę nazywał zdanie wykorzystane jako przesłanka w dowodzie, którego prawdziwość nie jest dyskutowana. Czasami zdanie to nie jest wyrażone wprost, ale jest zupełnie oczywiste, jest faktem empirycznym bądź językowym, np. że ojcem Sokratesa był Sofroniskos, albo że jeśli ktoś jest od kogoś starszy, to ta druga osoba jest młodsza odeń. Hipotezą nazywam przesłankę, która jest wątpliwa, a dowód przeprowadza się w celu zbadania jej konsekwencji. Czasem wątpliwości takie wychodzą dopiero w trakcie przeprowadzania dowodu, zwłaszcza po dojściu do sprzeczności lub po otrzymaniu zdania sprzecznego z faktami. Hipotezy pojawiają się we wszystkich dowodach niewprost.

3. Rozumowanie logiczne a rozumowanie poprawne

Kluczową dla niniejszej rozprawy jest dystynkcja pomiędzy rozumowaniem poprawnym a rozumowaniem logicznym, dlatego poświęcę jej trochę więcej miejsca.

W języku potocznym wniosek lub fakt nazywa się logicznym, jeżeli ma on uzasadnienie (tzn. może być przez kogoś poprawnie uzasadniony), niezależnie od podstaw tego uzasadnienia (założeń, jakie należy przyjąć by go poprawnie uzasadnić). W tym znaczeniu (potocznym) epitet „logiczny” jest używany jako antonim określenia (również potocznego) „bezsensowny”.

W dalszym ciągu niniejszej pracy epitet „logiczny”, gdy określa pojęcia takie jak „dowód” czy „rozumowanie”, jest używany w kontraście z takimi określeniami jak „matematyczny”, „arytmetyczny”, „fizyczny”, „meteorologiczny” lub „empiryczny”.

Tak więc dowód logiczny to taki dowód, którego formalizacja używa wyłącznie reguł logicznych, w którym wniosek można wydedukować z przesłanek na podstawie samej logiki, bez odwoływania się do wiedzy arytmetycznej, prawniczej lub jakiejkolwiek innej.

Logicy średniowieczni określali wnioskowanie logiczne terminem consequentia formalis, a pozostałe terminem consequentia materialis.

Oto najprostszy przykład formalizacji dowodu pozalogicznego:

(1)

.

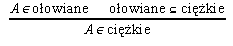Ten sam wniosek można też udowodnić za pomocą dwóch innych dowodów:

(2)

,

oraz:

(3)

,

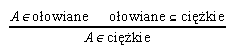Derywacja (1) jest przedstawieniem dowodu empirycznego, w którym jedyną zastosowaną regułą jest reguła empiryczna, pozwalająca na przejście od stwierdzenia „coś jest ołowiane” do stwierdzenia „to coś jest ciężkie”. W derywacji (2) jedyną zastosowaną regułą jest logiczna reguła odrywania (modus ponendo ponens). W derywacji (3) (która, skądinąd, na mocy definicji funktora „⊆”, jest na gruncie teorii mnogości równoważna poprzedniej) zastosowana jest pewna wersja sylogizmu „barbara”.

Derywacja pierwszego rodzaju (1) bywa zwana entymematem, czyli wnioskowaniem niepełnym. Ci którzy tak robią, utożsamiają ją z derywacją drugiego rodzaju ((2) lub (3)), twierdząc że druga przesłanka została przyjęta milcząco (domyślnie), jakkolwiek nie została wyrażona explicite.

Zwolennicy tej interpretacji sami przyjmują jednak domyślne założenie, że powinno się używać reguł logicznych zamiast pozalogicznych (zwanych dalej regułami specyficznymi). Można tymczasem równie dobrze powiedzieć odwrotnie, że derywacja (2) lub (3) to w istocie derywacja (1), tyle że błędnie nad kreską zapisano to, co zwykle się pisze równo z nią, jako uzasadnienie danego kroku:

(4)

.

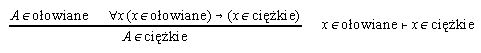Ponieważ wszystkie te derywacje są równie poprawne, należy dopuścić wszystkie interpretacje i przy wyborze formalizacji wybierać tę, która jest bliższa wysłowieniu dowodu.

Derywacja (1) będzie odpowiednią formalizacją dla dowodu w rodzaju następującego:

(5)

„Ta kula jest ciężka, bo jest ołowiana”.

Derywacja (2) jest formalizacją dowodu:

(6)

„Ta kula jest ołowiana; jeśli coś jest ołowiane, to jest ciężkie. Więc ta kula jest ciężka”.

Derywacja (3) dowodu:

(7)

„Ta kula jest ołowiana; wszystko ołowiane jest ciężkie. Więc ta kula jest ciężka”.

Derywacja (4) dowodu:

(8)

„Ta kula jest ołowiana, więc jest ciężka; wiem to stąd, że jeśli coś jest ołowiane, to jest ciężkie”.

Dowód logiczny (sformalizowany derywacjami (2) lub (3)) jest pierwotniejszy logicznie: do jego uznania wystarczy sama logika (z teorią mnogości), bez dodatkowych reguł specyficznych. Dowód specyficzny ((1) lub (4)) jest mniej ogólny, ale za to jest pierwotniejszy genetycznie: jest prostszy i łatwy do uzasadnienia empirycznego.

4. Wysłowienie reguły a jej użycie

Dowody (6) i (8) różnią się bardzo nieznacznie i często nie da się jednoznacznie określić, za pomocą której derywacji należy dany dowód sformalizować, by być bliżej intencji autora. Różnica jest tak subtelna, że najprawdopodobniej sam autor nie zdawał sobie z niej sprawy.

Wysłowieniem reguły będę nazywał rolę, jaką spełnia w derywacji (4) zdanie „x ∈ ołowiane ⊢ x ∈ ciężkie”. Użyciem reguły będę nazywał to samo (prawie) zdanie, zapisane w formie derywacji (1).

Tak więc dowody (6) i (8) różnią się tym, że w dowodzie (8) zdanie „jeśli coś jest ołowiane, to jest ciężkie” jest wysłowieniem reguły specyficznej, zaś w dowodzie (6) to samo zdanie jest częścią (jedną z przesłanek) użycia reguły logicznej.

Należy zauważyć, że jeżeli uznamy ową implikację w dowodzie (8) za wysłowienie reguły specyficznej, nie będziemy tu mieli do czynienia z zastosowaniem jakiejkolwiek reguły logicznej: reguła specyficzna (w której występują wyłącznie zdania proste z punktu widzenia logiki) będzie wysłowiona i zastosowana.

W tej pracy nie zajmuję się jednak stosowaniem reguł specyficznych: jest to zadaniem historyka prawa, fizyki, meteorologii etc., albo językoznawcy, zajmującego się znaczeniem i kolokacjami słowa „więc” i jemu pokrewnych. Nie leży to w polu zainteresowania historyka logiki. Dlatego też wnioskowania o charakterze prostych okresów warunkowych lub zdań wynikowych nie były brane pod uwagę w trakcie poszukiwań będących przedmiotem tej pracy.

Ponieważ jednak przedstawione tu badania miały na celu zebranie możliwie wszystkich przypadków zastosowań logiki w pismach przedarystotelesowych, we wszelkich sytuacjach, gdy możliwe były obie interpretacje dowodu, a więc możliwa była sytuacja, że autor traktował regułę specyficzną jako jedną z przesłanek stosowanej przez siebie reguły logicznej, dowód był traktowany jako logiczny, aby uniknąć niekompletności tego zbioru.

5. Historia logiki a historia filozofii

Między tymi dwiema dyscyplinami wiele jest podobieństw. Obie one są naukami historycznymi, empirycznymi, obie zajmują się analizowaniem wypowiedzi, a nie np. pozostałości materialnych jak niektóre inne dyscypliny historyczne. Wypowiedzi będące ich przedmiotem są dwojakiego rodzaju: explicite, gdzie definiuje się pojęcia, wyraża się twierdzenia, lub te twierdzenia się dowodzi, i implicite, gdzie używa się pojęć, presuponuje twierdzenia lub traktuje się inne twierdzenia jako dowiedzione.

Różnica między tymi naukami jest w tym, czego owe pojęcia, twierdzenia i dowody dotyczą. W przypadku historii filozofii są to pojęcia filozoficzne (byt, prawda, dobro, piękno etc.) i o nich twierdzenia, wreszcie tych twierdzeń dowody. W przypadku historii logiki są to pojęcia logiczne (konieczność, wynikanie, ważność etc.) i twierdzenia, prawa czy teorie logiczne, wreszcie takich twierdzeń dowody.

Clara non sunt interpretanda, jak głosi szacowna maksyma prawnicza: jeżeli coś jest wyrażone jasno, nie trzeba tego badać, wystarczy streścić lub zacytować. Dlatego właściwa praca historyka filozofii czy logiki zaczyna się wtedy, gdy w badanym materiale nie znajdujemy jasnych, explicite, wypowiedzi na dany temat i trzeba się zająć wypowiedziami implicite. Wtedy też dopiero najlepiej widać różnicę w badaniach historii logiki i historii filozofii. Praca napisana przez historyka filozofii to zbieranie cytatów i ich interpretowanie, szukanie pojęć i teorii filozoficznych, które mogły znaleźć w nich wyraz. Utwór historyka logiki to zbieranie dowodów, aby odtworzyć teorie logiczne, które mogły leżeć u ich podstaw. Dlatego praca napisana przez historyka logiki nie może przypominać zgrabnej prozy historyka filozofii i musi wyglądać tak, jak to widać w dalszym ciągu niniejszej rozprawy.

6. Historia logiki a filozofia logiki

Historia logiki, podobnie jak historia filozofii, jest nauką empiryczną, przeciwnie niż filozofia, w tym filozofia logiki, która jest nauką teoretyczną. Historia, w tym i historia logiki lub filozofii, zajmuje się ustalaniem faktów historycznych, podobnie jak np. historia polityczna. Filozofia, w tym i filozofia logiki, zajmuje się problemami ahistorycznymi, a to, że jakiś jej problem był poruszany w historii, nie ma dla niej znaczenia. Filozof czerpie często swoją problematykę z historii, ale ma to znaczenie wyłącznie dla jego biografów, a nie dla problematyki, którą się zajmuje.

Rozprawa nasza jest rozprawą historyczną, jej zadaniem nie jest więc roztrząsanie problemów samych w sobie, ale ustalanie faktów historycznych, podobnie jak jest to zadaniem historii filozofii lub historii politycznej.

7. Historia logiki a jej prehistoria

Za początkową datę w historii logiki przyjmuję (umownie) rok 350 p.n.e. Arystoteles miał wtedy 34 lata, było to już po napisaniu jego — zaginionych — platonizujących dialogów filozoficznych, przystępował wtedy zapewne do pisania Topik, najstarszego z dzieł Organonu. Platon wprawdzie jeszcze wtedy żył, ale miał już 77 lat i po trzech latach zmarł (po jego śmierci Arystoteles opuścił Ateny na dwanaście lat).

Ponieważ Organon jest najstarszym zachowanym traktatem logicznym (ściśle mówiąc, zbiorem traktatów), moment powstania pierwszych jego części jest dobrą datą wyznaczającą początek dziejów logiki. Wszystkie wcześniejsze fakty odnoszące się do logiki będę więc zaliczał do jej prehistorii.

Istotne jest jeszcze jedno ograniczenie, jakie jest narzucone na całość niniejszych badań: dziedzina poszukiwań jest ograniczona do krajów kultury greckiej, czyli Grecji właściwej i jej kolonii. Powody, dla których literatura w innych językach nie została wzięta pod uwagę, poza ich nieznajomością przez autora, jest następujący: Grecy byli (przynajmniej od czasów wojen perskich) dość mocno zamknięci na wpływy zewnętrzne, bardzo mało jest więc prawdopodobne, że jakieś (zachowane) teksty obcojęzyczne mogły mieć wpływ na Arystotelesa, tym bardziej że zachowało się tych tekstów dość mało w porównaniu z w miarę zwartym zbiorem klasycznych tekstów greckich. Można jeszcze dodać, że tylko Grecy wykształcili w starożytności nauki teoretyczne, w tym filozofię, logikę i geometrię, trudno więc przypuszczać, by w tekstach innojęzycznych z tamtego okresu można było znaleźć cokolwiek wartościowego z punktu widzenia niniejszych badań.

Autorów zachowanych pism greckich sprzed roku 350 p.n.e. będę nazywał prearystotelikami.