II. Zależności statystyczne

Marek Jerzy. Minakowski, Prehistoria logiki formalnej

I. Fragmenta prearistotelicorum

2. System przyjęty w formalizacji

Używam notacji ideograficznej (⊆, ∥, ⊈, ∦) ze względów praktycznych. Używanie symboliki tradycyjnej (A, E, I, O) utrudniłoby odczytywanie zdań, w których terminami są całe wyrazy (lub nawet ich grupy), a nie symbole literowe.

Wszystkie reguły są podane tylko w jednym miejscu, na następnej stronie. W dowodzie podawany jest tylko numer wykorzystanej reguły, w którym zakodowane są pewne jej cechy. Wyjaśnienie ich podane jest w następnym punkcie.

Zapis reguł

Nad kreską wypisane są przesłanki (jedna nad drugą), pod kreską wniosek (jak w klasycznej sylogistyce); w regułach zdaniowych symbole równokształtne w miarę możliwości zapisywane są w jednej linii pionowej. W inny sposób zapisywane są dowody niewprost: przesłanki wypisane są poziomo nad kreską; jedną z przesłanek jest tu dowód, oznaczony przez 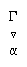, gdzie Γ jest listą przesłanek, a α wnioskiem. Terminy są nazywane w kolejności wystąpienia.

Język

Zmienne

1. nazwowe: A, B, C, …
2. zdaniowe: α, β, γ, …

Funktory

1. Zdaniotwórcze
   1. funktory zdaniotwórcze od argumentów zdaniowych

      → implikacja (1-argumentowy)

      ~ negacja zdaniowa (2-arg.)

      ∧ koniunkcja zdaniowa (2-arg.)

      ∨ alternatywa łączna zdaniowa (2-arg.)

      ⊻ alternatywa rozłączna zdaniowa (2-arg.)

      ≡ równoważność (2-arg.)

   2. funktory zdaniotwórcze od argumentów nazwowych (2-argumentowe)

      ⊆ słaba inkluzja (inkluzja lub identyczność)

      = identyczność (równozakresowość)

      ∦ nierozłączność (przecinanie się)

      ∥ rozłączność (brak części wspólnej)

      ⊈ negacja słabej inkluzji (nie inkluzja i nie identyczność)

      ≠ negacja identyczności (nieidentyczność)

   3. funktor zdaniotwórczy bezargumentowy

      ⊥ sprzeczność (absurd)

2. Nazwotwórcze
   1. funktory nazwotwórcze od argumentów nazwowych

      ¬ negacja nazwowa (dopełnienie mnogościowe: 1-arg.)

      ∩ koniunkcja nazwowa (iloczyn mnogościowy: 2-arg.)

      ∪ alternatywa nazwowa (suma mnogościowa: 2-arg.)

   2. funktory specyficzne, oznaczane jak zmienne nazwowe

      — funktory nazwotwórcze specyficzne, oznaczane jak zmienne nazwowe (mogą być też traktowane jak zmienne predykatywne)