Summary: The Pre-Aristotelian Formal Logic
Część I - Logika formalna przed Arystotelesem
- Wstęp
- Objaśnienia ważniejszych pojęć
- Wybrane dotychczasowe ujęcia przedarystotelesowej logiki formalnej
- Plan badań i metodologia
- Opis zgromadzonego materiału źródłowego
- Fragmenta praearistotelicorum — przykłady
- Analiza wyników
- Rozstrzygnięcia
- Bibliografia
Część II - Katalog przedarystotelesowych fragmentów logicznych
I. Fragmenta prearistotelicorum
- Układ pozycji katalogowej
- System przyjęty w formalizacji
- Reguły logiczne znalezione u prearystotelików
- Kanon pism prearystotelików
- Spis znalezionych fragmentów logicznych w pismach prearystotelików
- Katalog fragmentów logicznych znalezionych w pismach prearystotelików
- Dodatek 1.: fragmenty logiczne we fragmentach presokratyków
- Dodatek 2.: fragmenty logiczne w pismach pseudoplatońskich
Marek Jerzy. Minakowski, Prehistoria logiki formalnej
II. Zależności statystyczne
1. Nasycenie tekstu logiką
Tabela 1. przedstawia różne parametry określające stopień nasycenia różnych utworów logiką. Są to: ilość znalezionych fragmentów logicznych (B), ilość zastosowanych reguł (C), ilość kroków dowodowych (D) oraz suma długości fragmentów logicznych (E). Wszystkie te wielkości są odniesione do całkowitej długości tekstu (A), wyznaczonej na podstawie Thesaurus Linguae Graece (zmierzonej za pomocą programu Musaios).
Ksenofont i Platon zostali rozbici na poszczególne utwory, dzieła pozostałych autorów zostały potraktowane razem. Na końcu tabeli znajduje się podsumowanie dla różnych rodzajów literackich; z wyjątkiem Ksenofonta każdy autor zalicza się do jednego rodzaju literackiego (pisma Ksenofonta są częściowo w filozofii, częściowo w historii). Podział na rodzaje literackie jest częściowo umowny, jako że te pisma Hipokratesa (O sztuce i O naturze ludzkiej), w których zachowały się dowody logiczne, mają charakter typowo filozoficzny (z kręgu Gorgiasza). Podobnie mowy Antyfonta zawierające dowody logiczne (Tetralogie) nie były przeznaczone do wygłoszenia, stanowiły teoretyczny przykład, jak należy mowy pisać (być może sam Antyfon nie zdawał sobie sprawy z ich sztuczności).
Tabela 1. Nasycenie tekstu logiką
| L.p. | Tytuł | długość tekstu A | ilość fragm. B | ilość reguł C | ilość kroków D | długość fragmentów E | E/A ×10.000 F | B/A ×3000.000 G | C/A ×2000.000 H | D/A ×1000.000 I |
| I. | Ajschylos | 374 814 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| II. | Andokides | 141 816 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| III. | Antyfon | 144 259 | 3 | 9 | 22 | 1 818 | 126 | 62 | 125 | 153 |
| IV. | Arystofanes | 925 386 | 3 | 3 | 11 | 1 387 | 15 | 10 | 6 | 12 |
| V. | Demostenes | 837 233 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| VI. | Eurypides | 1 321 912 | 2 | 1 | 4 | 771 | 6 | 5 | 2 | 3 |
| VII. | Herodot | 1 491 375 | 5 | 6 | 22 | 2 478 | 17 | 10 | 8 | 15 |
| VIII. | Hezjod | 129 260 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| IX. | Hipokrates | 871 647 | 3 | 8 | 21 | 1 307 | 15 | 10 | 18 | 24 |
| X. | Homer | 1 714 469 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| XI. | Izajos | 182 266 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| XII. | Izokrates | 746 309 | 1 | 1 | 3 | 237 | 3 | 4 | 3 | 4 |
| XIII. | Ksenofont | 2 478 638 | 15 | 39 | 112 | 11 230 | 45 | 18 | 31 | 45 |
| 192. | Historia grecka | 539 189 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 193. | Wspomnienia o Sokratesie | 278 969 | 9 | 24 | 68 | 6 373 | 228 | 97 | 172 | 244 |
| 194. | Ekonomik | 137 059 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 195. | Uczta | 72 487 | 1 | 6 | 17 | 1 061 | 146 | 41 | 166 | 235 |
| 196. | Obrona Sokratesa | 15 749 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 197. | Anabaza | 454 082 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 198. | Cyropedia | 612 402 | 4 | 6 | 20 | 3 192 | 52 | 20 | 20 | 33 |
| 199. | Hieron | 46 539 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 200. | Agesilaos | 59 146 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 201. | Rzeczpospolita Lacedemońska | 39 487 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 202. | O dochodach | 30 356 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 203. | Dowódca kawalerii | 45 324 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 204. | O jeździectwie | 52 883 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 205. | O łowiectwie | 70 298 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 206. | Rzeczpospolita Ateńska | 24 668 | 1 | 3 | 7 | 604 | 245 | 122 | 243 | 284 |
| XIV. | Lizjasz | 421 293 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| XV. | Platon | 4 419 430 | 127 | 330 | 899 | 101 784 | 230 | 86 | 149 | 203 |
| 241. | Eutyfron | 40 451 | 1 | 2 | 4 | 356 | 88 | 74 | 99 | 99 |
| 242. | Obrona Sokratesa | 67 317 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 243. | Kriton | 32 428 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 244. | Fedon | 168 611 | 8 | 17 | 42 | 6 051 | 359 | 142 | 202 | 249 |
| 245. | Kratylos | 145 976 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 246. | Teajtet | 182 487 | 10 | 36 | 83 | 9 670 | 530 | 164 | 395 | 455 |
| 247. | Sofista | 135 063 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 248. | Polityk | 143 820 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 249. | Parmenides | 114 526 | 12 | 58 | 140 | 11 911 | 1040 | 314 | 1013 | 1222 |
| 250. | Fileb | 145 512 | 1 | 2 | 5 | 567 | 39 | 21 | 27 | 34 |
| 251. | Uczta | 132 989 | 4 | 8 | 21 | 2 418 | 182 | 90 | 120 | 158 |
| 252. | Fajdros | 131 161 | 1 | 2 | 8 | 987 | 75 | 23 | 30 | 61 |
| 253. | Alkibiades I | 86 463 | 8 | 12 | 43 | 3 418 | 395 | 278 | 278 | 497 |
| 254. | Alkibiades II | 34 100 | 1 | 1 | 3 | 485 | 142 | 88 | 59 | 88 |
| 255. | Hipparch | 18 761 | 2 | 4 | 12 | 1 373 | 732 | 320 | 426 | 640 |
| 256. | Rywale | 18 905 | 1 | 1 | 4 | 737 | 390 | 159 | 106 | 212 |
| 257. | Teages | 27 757 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 258. | Charmides | 62 761 | 9 | 12 | 37 | 4 563 | 727 | 430 | 382 | 590 |
| 259. | Laches | 60 255 | 2 | 3 | 8 | 1 201 | 199 | 100 | 100 | 133 |
| 260. | Lyzis | 52 806 | 1 | 3 | 14 | 1 005 | 190 | 57 | 114 | 265 |
| 261. | Eutydem | 97 241 | 14 | 26 | 77 | 10 425 | 1072 | 432 | 535 | 792 |
| 262. | Protagoras | 136 642 | 7 | 12 | 38 | 4 199 | 307 | 154 | 176 | 278 |
| 263. | Gorgiasz | 210 628 | 8 | 25 | 75 | 8 946 | 425 | 114 | 237 | 356 |
| 264. | Menon | 79 367 | 3 | 12 | 30 | 6 399 | 806 | 113 | 302 | 378 |
| 265. | Hippiasz większy | 66 199 | 6 | 23 | 58 | 6 866 | 1037 | 272 | 695 | 876 |
| 266. | Hippiasz mniejszy | 34 071 | 3 | 10 | 32 | 4 251 | 1248 | 264 | 587 | 939 |
| 267. | Ijon | 30 891 | 2 | 3 | 8 | 964 | 312 | 194 | 194 | 259 |
| 268. | Meneksenos | 38 573 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 269. | Klejtofon | 12 140 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 270. | Rzeczpospolita I | 75 983 | 4 | 24 | 59 | 5 979 | 787 | 158 | 632 | 776 |
| 271. | Rzeczpospolita II–IX | 533 271 | 3 | 7 | 19 | 1 979 | 37 | 17 | 26 | 36 |
| 272. | Rzeczpospolita X | 69 542 | 4 | 7 | 19 | 2 299 | 331 | 173 | 201 | 273 |
| 273. | Timajos | 181 749 | 8 | 12 | 38 | 3 410 | 188 | 132 | 132 | 209 |
| 274. | Krytiasz | 38 197 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 275. | Minos | 23 304 | 2 | 6 | 16 | 863 | 370 | 257 | 515 | 687 |
| 276. | Prawa | 810 241 | 2 | 2 | 6 | 462 | 6 | 7 | 5 | 7 |
| 277. | Epinomis | 47 893 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 278. | Listy | 131 349 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| XVI. | Sofokles | 518 086 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| XVII. | Tukidydes | 1 214 352 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Epika | 1 843 729 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Tragedia | 2 214 812 | 2 | 1 | 4 | 771 | 3 | 3 | 1 | 2 | |
| Komedia | 925 386 | 3 | 3 | 11 | 1 387 | 15 | 10 | 6 | 12 | |
| Retoryka | 2 473 176 | 4 | 10 | 25 | 2 055 | 8 | 5 | 8 | 10 | |
| Medycyna | 871 647 | 3 | 8 | 21 | 1 307 | 15 | 10 | 18 | 24 | |
| Historia | 3 698 998 | 5 | 6 | 22 | 2 478 | 7 | 4 | 3 | 6 | |
| Filozofia | 5 904 797 | 142 | 369 | 1011 | 113 014 | 191 | 72 | 125 | 171 | |
| Wszystko | 17 932 545 | 159 | 397 | 1094 | 121 012 | 67 | 27 | 44 | 61 | |
Te dane wskazują na ogromną dysproporcję pomiędzy częstością używania logiki przez filozofów (zwłaszcza w utworach sokratycznych Platona i Ksenofonta) i innych pisarzy. Przyjmijmy dla uproszczenia, że na jednej stronie mieści się 2000 znaków (bez spacji), wtedy jedno zastosowanie reguły logicznej zdarza się raz na 8 stron w literaturze filozoficznej, zaś raz na 215 w pozostałych tekstach (wszystkie zachowane teksty prearystotelików w tym corpus to 8699 stron). A więc można powiedzieć, że filozofowie używali logiki 27 razy częściej niż wszyscy inni! Po odjęciu Praw i Rzeczypospolitej II–X Platona oraz Cyropedii Ksenofonta uzyskamy jeszcze więcej: w tekstach filozoficznych jedno użycie reguły logicznej przypada na 5,7 strony — w tych utworach razem wziętych jedna reguła przypada na 46 stron. Gdyby z kolei z tekstów pozafilozoficznych odjąć krótkie utwory teoretyczne przypisywane Hipokratesowi (O sztuce i O naturze ludzkiej) oraz „mowy” szkolne Antyfonta (Tetralogie), to okazuje się, że w tekstach pozafilozoficznych jedno użycie reguły logicznej przypada na 542 strony!
Dla historii i tragedii (a zatem dla tekstów pozafilozoficznych w ogóle) wielkości odwołujące się do liczby fragmentów logicznych i ich długości (kolumny B, E, F i G) są trochę zawyżone, jako że uwzględnione tam zostały fragmenty nie zawierające żadnej reguły logicznej.
2. Wzrost i upadek logiki Platona
Dane z tabeli 1. zostały wykorzystane do zbadania jak zmieniała się w czasie częstość używania logiki w przypadku Platona. Wykorzystałem w tym celu wyniki G.R. Ledgera, który dokonał najpełniejszej analizy stylometrycznej utworów Platona.
Spośród utworów należących do tetralogii Trazyllosa Ledger nie uwzględnia tylko Alkibiadesa II, choć uznaje go za raczej autentyczny; dołączam go tu zaraz po Alkibiadesie I: nawet jeżeli ów krótki utwór jest nieautentyczny, to naśladuje on Alkibiadesa I, można więc umieścić je razem. Wszystkie listy umieszczam tam, gdzie Ledger umieścił najdłuższy z nich, VII.
Kolejno powstałe utwory Platona zostały podzielone przeze mnie na grupy, po około 0,5 mln znaków. Grupy zawierające Rzeczpospolitą i Prawa mają po około 1 mln znaków, ale za to na wykresie są powtórzone. W ten sposób wykres jest w miarę adekwatnym przedstawieniem zmian, jakie zachodziły w użyciu logiki przez Platona.
W wyniku komputerowej analizy stylu Platona Ledger uzyskał wynik, zgodnie z którym Rzeczpospolita winna być przed Parmenidesem i Teajtetem; w imię zgodności z powszechną opinią umieścił ją jednak później. Rozwiązuję to w ten sposób, że I księgę Rzeczypospolitej włączam do wcześniejszej grupy (z Parmenidesem), a resztę do późniejszej (z Teajtetem).
Kolejność powstawania utworów Platona według Ledgera (podział na grupy pochodzi ode mnie, przedziały czasowe są wyłącznie orientacyjne, stypulowane na podstawie wyników Ledgera):
1.
Lysis, Eutyfron, (Minos), Hippiasz Mniejszy, Ijon, Hippiasz Większy, Alkibiades I, Alkibiades II, Teages, Kriton (399–390)
2.
Gorgiasz, Meneksenos, Menon, Charmides, Obrona Sokratesa (390–385)
3.
Fedon, Laches, (Hipparch), (Rywale), Protagoras, Eutydem (385–380)
4.
Uczta, Kratylos, Rzeczpospolita I, Parmenides (380–370)
5.
Teajtet, Rzeczpospolita II–X, Fajdros (370–360)
6.
Fileb, Klejtofon, Listy, Sofista, Polityk (355–352)
7.
Prawa, Epinomis, Timajos, Krytiasz (351–347)
Analizy Ledgera wykazały, że być może trzy dialogi Platona nie są autentyczne, ich język odstaje bowiem dość wyraźnie od języka pozostałych utworów; są to Minos, Hipparch i Rywale. Nie wynika stąd, że na pewno są one fałszerstwami; nie biorę ich tu jednak pod uwagę, aby nie wchodzić w niepotrzebne spory.
Osobno podaję wartości dla grupy 4 z wyłączeniem fr. 53 (Parmenides 137c4–142a6) jako grupy 4a. Fragment 53. (8102 znaki) sam zawiera 47 reguł w 102 krokach. Został dokładniej omówiony w Dodatku 3.
Tabela 2. Częstość użycia logiki w kolejnych okresach życia Platona wg Ledgera
| Okres | długość tekstu A | ilość fragmentów B | ilość reguł C | ilość kroków D | długość fragmentów E | E/A ×10.000 F | B/A ×3000.000 G | C/A ×2000.000 H | D/A ×1000.000 I |
| Całość | 4 358 455 | 122 | 319 | 867 | 98 806 | 227 | 84 | 146 | 199 |
| 1. | 405 161 | 22 | 54 | 162 | 17 340 | 428 | 163 | 267 | 400 |
| 2. | 458 646 | 20 | 49 | 142 | 19 908 | 434 | 131 | 214 | 310 |
| 3. | 462 749 | 31 | 58 | 165 | 21 876 | 473 | 201 | 251 | 357 |
| 4. | 469 474 | 20 | 89 | 220 | 20 308 | 433 | 128 | 379 | 469 |
| 4a | 461 264 | 19 | 42 | 118 | 12 098 | 262 | 124 | 182 | 256 |
| 5. | 916 461 | 18 | 53 | 129 | 14 935 | 163 | 59 | 116 | 141 |
| 6. | 567 884 | 1 | 2 | 5 | 567 | 10 | 5 | 7 | 9 |
| 7. | 1 078 080 | 10 | 14 | 44 | 3 872 | 36 | 28 | 26 | 41 |
Wykres 1. Względna długość fragmentów logicznych (F), względna ilość kroków dowodowych (I), reguł (H) i fragmentów logicznych (G) w kolejnych grupach utworów Platona (czas powstania wg Ledgera)
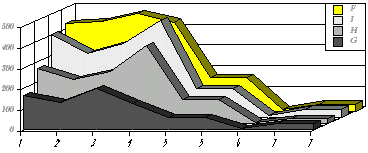
Wykres 2. Te same dane, tylko zamiast grupy 4. jest grupa 4a (tzn. nie jest uwzględniony na wykresie fragment 53.)
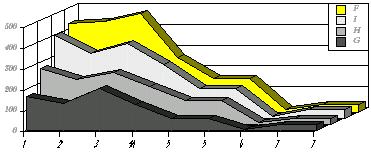
Z tych wykresów wynika kilka bardzo ważnych wniosków dla historii logiki. Pierwszym jest to, że maksymalne nasycenie logiką jego utworów ma miejsce w utworach najwcześniejszych: nie widać u Platona żadnego rozwoju. Można to interpretować jako skutek starzenia się, ale byłaby to interpretacja złośliwa. Ważniejsze jest to innego: wygląda na to, że wszystko, co Platon umiał w logice, umiał już na samym początku, zanim się zabrał do pisania. Nauczył się tego zatem od swojego mistrza. Mamy więc bardzo silną wskazówkę, że to Sokrates był autorem zastosowań logiki w filozofii, a Platon w miarę swego życia odchodził od niej.
Widać, poprzez porównanie obydwu wykresów, jak bardzo fragment 53. odstaje od reszty twórczości Platona tego okresu.
Zestawieniom tym można postawić kilka zarzutów. Po pierwsze: opierają się na czysto mechanicznym liczeniu różnych cech gramatycznych języka różnych utworów. Bardzo mało mamy informacji na temat dat powstania różnych utworów Platona; powyższe ustalenie kolejności ich powstania opiera się w całości na hipotezie Lutosławskiego, że język Platona zmieniał się z czasem we w miarę stałym tempie i w sposób jednokierunkowy. Możliwe jest, że takie mechaniczne ustalanie sekwencji utworów Platona jest niewłaściwe, a lepsze wyniki uzyskałoby się porównując treść tych utworów. Innym poważnym zarzutem jest, że w tym zestawieniu znajduje się kilka utworów, które są dość powszechnie uznawane za nieautentyczne, pochodzące od autora innego niż Platon.
Z pierwszym z tych zarzutów można polemizować, odwołując się do faktu, że właściwie wszystko, co wiemy o rozwoju Platona, wywodzi się z badań Lutosławskiego nad jego stylem. Dopiero on ustalił, że teoria idei była charakterystyczna dla średniego okresu życia Platona, a później została zarzucona na rzecz koncepcji pitagorejskich. Na zarzut drugi można odpowiedzieć w ten sposób, że bardzo nieliczne utwory znane pod imieniem Platona nie były nigdy przedmiotem ataku ze względu na ich sugerowaną nieautentyczność.
Mimo wszystko przedstawię tu także inny podział utworów Platona. Jest to tradycyjny, szkolny układ Izydory Dąmbskiej. Podzieliła ona utwory Platona na cztery okresy:
1.
Śladami Sokratesa: Eutyfron, Obrona Sokratesa, Kriton, Ion, Protagoras, Laches, Lizys, Charmides
2.
Walka z sofistyką i kształtowanie się własnych poglądów: Hippiasz Mniejszy, Hippiasz Większy, Gorgiasz, Menon, Eutydem, Kratylos, Meneksenos
3.
Pełnia rozkwitu: Uczta, Fajdros, Fedon, Rzeczpospolita, Teajtet
4.
U schyłku życia: Parmenides, Sofista, Polityk, Fileb, Timajos, Kritiasz, Listy, Prawa
Do grupy piątej zaliczyłem pozostałe utwory Platona, nieuwzględnione przez Dąmską (głównie ze względu na ich powątpiewalną autentyczność oraz nieistotność filozoficzną): Alkibiades I i II, Epinomis, Teages, Hipparch, Minos, Rywale, Klejtofon
Przy analizie wykresu należy zwrócić uwagę, że każda z czterech grup jest obszerniejsza od poprzedniej (czwarta jest trzykrotnie większa niż pierwsza). Dlatego grupa trzecia jest na wykresie przedstawiona podwójnie, a czwarta potrójnie.
Grupa 4a oznacza, podobnie jak poprzednio, grupę 4. bez fr. 53 (całość = 1+2+3+4+5).
Tabela 3. Częstość użycia logiki w kolejnych okresach życia Platona wg Dąmbskiej
| L.p. | Tytuł | długość tekstu A | ilość fragm. B | ilość reguł C | ilość kroków D | długość fragmentów E | E/A ×10.000 F | B/A ×3000.000 G | C/A ×2000.000 H | D/A ×1000.000 I |
| Całość | 4 419 430 | 127 | 329 | 900 | 101 784 | 230 | 86 | 149 | 204 | |
| 1. | Śladami Sokratesa | 483 551 | 22 | 35 | 109 | 12 288 | 254 | 136 | 145 | 225 |
| 2. | Walka z sofistyką i kształtowanie się własnych poglądów | 672 055 | 34 | 96 | 272 | 36 887 | 549 | 152 | 286 | 405 |
| 3. | Pełnia rozkwitu | 1 294 044 | 34 | 101 | 252 | 29 383 | 227 | 79 | 156 | 195 |
| 4. | U schyłku życia | 1 700 457 | 23 | 73 | 189 | 16 350 | 96 | 41 | 86 | 111 |
| 4a | — bez fr. 53. | 1 692 247 | 22 | 26 | 87 | 8 140 | 48 | 39 | 31 | 51 |
| 5. | Inne | 269 323 | 14 | 24 | 78 | 6 876 | 255 | 156 | 178 | 290 |
Wykres 3. Względna długość fragmentów logicznych (F), względna ilość kroków dowodowych (I), reguł (H) i fragmentów logicznych (G) w kolejnych grupach utworów Platona (czas powstania wg Dąmbskiej)
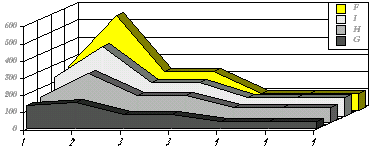
Wykres 4. Te same dane, co poprzednio, tylko zamiast grupy 4. jest grupa 4a (tzn. nie jest uwzględniony na wykresie fragment 53.)

Jak widać, główną różnicą jest tu znaczna przewaga grupy drugiej nad pozostałymi; jednak wnioski ogólne będą tu takie same: w wieku dojrzałym Platon zaprzestał używania logiki.
3. Układ terminów w regułach
Następne tabele dotyczą różnych klasyfikacji reguł użytych we fragmentach. Pierwsza z nich przeprowadzona jest według układu zmiennych.
Zmienne mogą być dwojakiego rodzaju: zdaniowe lub nazwowe. Reguły zawierające wyłącznie zmienne zdaniowe lub oba rodzaje zmiennych są zakwalifikowane do dwóch osobnych grup. Reguły operujące wyłącznie zmiennymi nazwowymi (zwanymi tradycyjnie terminami) zostały podzielone wedle wzajmenego ich układu, zwanego tradycyjnie figurą sylogistyczną.
Pamiętać należy, że w tekście tak samo wygląda podstawienie zmiennej zdaniowej, jak i zdania ze zmiennymi nazwowymi; to czy zdanie „Sokrates jest człowiekiem” jest potraktowane jako podstawienie zmiennej zdaniowej α, czy podstawienie S/Sokrates i P/człowiek w formule „S jest P” za zmienne nazwowe S i P, zależy wyłącznie od funkcji spełnianej przez to zdanie w dowodzie.
Oznaczenie figury sylogistycznej („_” zastępuje wszystkie funktory zdaniotwórcze od dwóch argumentów nazwowych)
- konsekwencja i konwersja
cons conv 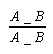
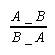
- klasyczne figury sylogistyczne:
I II III IV 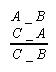
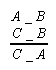
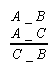
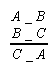
- figury z przestawionymi przesłankami:
Im IIm IIIm IVm 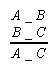
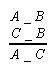
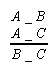
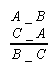
- sylogizmy skondycjonalizowane (sylogizmy o wniosku warunkowym) figury Xc powstają z sylogizmów figury X poprzez usunięcie ostatniej przesłanki i zastąpienie konkluzji implikacją, której poprzednikiem jest owa usunięta przesłanka, a następnikiem wniosek konkluzji sylogizmu fig. X. Na przykład z figury IIm otrzymujemy figurę IImc:
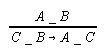 ;
;
- łańcuszniki: sylogizmy o więcej niż dwóch przesłankach, oznaczane „sorx”, gdzie x jest liczbą przesłanek;
- funktora nazwotwórczego od jednego argumentu nazwowego „¬” nie bierze się pod uwagę (figura jest oznaczana tak, jakby go nie było)
- inne funktory nazwotwórcze od jednego argumentu nazwowego są również ignorowane, ale takie reguły są oznaczane „X obl”, gdzie X jest oznaczeniem figury, do której należałaby dana reguła, gdyby ich nie było. Oznaczenie „obl.” pochodzi od tradycyjnego określenia takich reguł jako „sylogizmy o terminie w przypadku zależnym” (łac. casus obliquus), co jest błędnie tłumaczone na „sylogizmy ukośne”.
Osobno są potraktowane reguły zawierające funtory nazwotwórcze od dwóch argumentów nazwowych (∩ i ∪): tworzą one sylogizmy o terminach złożonych (w opozycji do nich pozostałe są zwane sylogizmami o terminach prostych)
Tabela 4. Wg miejsc
Miejsca oznaczają numer fragmentu
| figura | miejsca | ilość miejsc |
| cons | 43 | 1 |
| cons obl | 301, 301, 305 | 3 |
| Razem cons | 4 | |
| conv | 25, 25, 48, 48, 53, 53, 53, 121, 126, 128, 133, 134, 157, 303 | 14 |
| Razem conv | 14 | |
| Razem jednoprzesłankowe reguły nazwowe o terminach prostych | 18 | |
| 1 | 3, 18, 18, 23, 27, 40, 41, 42, 42, 43, 45, 46, 46, 64, 68, 71, 74, 74, 79, 79, 95, 95, 100, 103, 103, 104, 105, 107, 107, 123, 123, 125, 126, 127, 127, 133, 134, 135, 137, 137, 137, 140, 148, 217, 217 | 45 |
| 1m | 14, 18, 20, 22, 22, 27, 29, 34, 37, 39, 43, 45, 46, 48, 50, 51, 53, 53, 57, 60, 64, 67, 84, 91, 96, 98, 99, 99, 101, 110, 112, 116, 116, 120, 120, 123, 125, 125, 125, 126, 129, 129, 129, 140, 140, 140, 141, 141, 141, 146, 146, 147, 150, 153, 158, 159, 208, 217, 301, 301 | 60 |
| 1 obl | 31, 31, 31, 119 | 4 |
| 1m obl | 137, 137, 141 | 3 |
| 1c | 16, 38, 38, 38, 53, 53, 56, 58, 216, 219, 220 | 11 |
| 1mc | 218 | 1 |
| Razem figura I | 124 | |
| 2 | 14, 17, 18, 18, 18, 18, 26, 26, 26, 33, 35, 37, 53, 53, 53, 70, 83, 85, 88, 91, 96, 111, 115, 124, 125, 133, 137, 142, 143, 144, 145, 148, 149, 156, 156, 217, 217, 218 | 38 |
| 2m | 26, 26, 33, 46, 47, 48, 50, 50, 51, 53, 53, 53, 67, 76, 76, 82, 92, 98, 101, 129, 144, 152, 156, 207, 207, 219, 302 | 27 |
| 2 obl | 68 | 1 |
| 2m obl | 66, 137, 137, 137, 139 | 5 |
| 2c | 9, 218, 219, 220, 220, 220 | 6 |
| Razem figura II | 77 | |
| 3 | 51, 74, 87, 88, 117, 301, 306 | 7 |
| 3m | 51, 86, 114, 120, 129, 133, 301 | 7 |
| 3mc | 32, 51 | 2 |
| Razem figura III | 16 | |
| 4 | 51, 108 | 2 |
| 4 obl | 79 | 1 |
| Razem figura IV | 3 | |
| Razem dwuprzesłankowe reguły nazwowe o terminach prostych | 220 | |
| sor3 | 8, 15, 21, 25, 25, 27, 27, 27, 27, 32, 46, 53, 54, 61, 65, 69, 72, 73, 93, 93, 94, 102, 108, 113, 114, 120, 121, 121, 121, 128, 129, 131, 131, 133, 148, 155, 156, 301 | 38 |
| sor3 obl | 19, 31, 119, 119, 137 | 5 |
| sor3c | 53 | 1 |
| Razem trójprzesłankowe reguły nazwowe o terminach prostych | 44 | |
| sor4 | 5, 22, 36, 46, 62, 69, 80, 97, 99, 99, 141, 303 | 12 |
| sor4 obl | 151, 305 | 2 |
| Razem czteroprzesłankowe reguły nazwowe o terminach prostych | 14 | |
| sor5 | 93, 102, 132, 304 | 4 |
| Razem pięcioprzesłankowe reguły nazwowe o terminach prostych | 4 | |
| sor9 | 77 | 1 |
| Razem dziewięcioprzesłankowe reguły nazwowe o terminach prostych | 1 | |
| Razem reguły nazwowe o terminach prostych | 301 | |
| compl | 14, 28, 53, 53, 53, 53, 76, 107, 112, 118, 118, 118, 120, 120, 121, 124, 124, 125, 138, 138, 140, 154, 156, 209 | 24 |
| compl obl | 53, 119, 138, 138 | 4 |
| Razem reguły nazwowe o terminach złożonych | 28 | |
| KRZ | 1, 1, 1, 1, 1, 2, 2, 4, 6, 9, 10, 11, 12, 14, 16, 16, 24, 32, 35, 37, 38, 38, 38, 43, 44, 45, 49, 51, 51, 51, 51, 52, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 55, 63, 66, 75, 78, 88, 90, 99, 101, 108, 108, 122, 129, 130, 130, 130, 130, 131, 136, 136, 149, 153, 201, 202, 203, 204, 205, 206, 207, 207, 207, 207, 207, 210, 211, 212, 213, 213, 213, 213, 213, 213, 213, 213, 214, 214, 214, 215, 215, 215, 307, 307, 307, 307, 307, 307 | 104 |
| Razem reguły bez terminów nazwowych (wyłącznie zdaniowe) | 104 | |
| inna | 3, 10, 40, 44, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 59, 66, 81, 86, 89, 108, 119, 121, 126, 130, 133, 134, 138, 138, 140, 140, 146, 216, 216, 216 | 35 |
| Razem reguły pozostałe | 35 | |
| Razem | 468 | |
Tabela 5. Reguły nazwowe o terminach prostych według grup tekstów
Grupy oznaczają:
1–4 teksty pozafilozoficzne
1 dramat
2 retoryka
3 medycyna
4 historia
5–17 teksty filozoficzne, w tym:
5–12 teksty sokratyków
5 Ksenofont
6 Platon, okres I (co do chronologii Platona, patrz wyżej)
7 Platon, okres II
8 Platon, okres III
9 Platon, okres IV, bez fr. 53
10 Platon, okres V
11 Platon, okres VI
12 Platon, okres VII
13 Eleaci
14 Platon, fr. 53
15–17 inni presokratycy
15 Gorgiasz
16 Dissoi logoi
16 inni
18 Pseudo-Platon
Do Corpus prearystotelików należą grupy 1–12 i 14. Fragmenty presokratyków to grupy 13 i 15–17.
| figura | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| cons | 1 | 1 | 1 | 1 | |||||||||||||||||||
| cons obl | 3 | 3 | |||||||||||||||||||||
| Razem cons | 1 | 1 | 1 | 3 | 4 | ||||||||||||||||||
| conv | 13 | 10 | 2 | 5 | 1 | 2 | 3 | 1 | 14 | ||||||||||||||
| Razem conv | 13 | 10 | 2 | 5 | 1 | 2 | 3 | 1 | 14 | ||||||||||||||
| Razem jednoprzesłankowe | 14 | 11 | 2 | 5 | 1 | 3 | 3 | 4 | 18 | ||||||||||||||
| 1 | 1 | 1 | 44 | 42 | 4 | 9 | 3 | 13 | 5 | 6 | 1 | 1 | 2 | 2 | 45 | ||||||||
| 1m | 1 | 1 | 57 | 53 | 6 | 4 | 9 | 11 | 6 | 12 | 1 | 4 | 2 | 2 | 1 | 1 | 2 | 60 | |||||
| 1 obl | 4 | 4 | 3 | 1 | 4 | ||||||||||||||||||
| 1m obl | 3 | 3 | 2 | 1 | 3 | ||||||||||||||||||
| 1c | 1 | 1 | 10 | 5 | 3 | 2 | 2 | 3 | 1 | 2 | 11 | ||||||||||||
| 1mc | 1 | 1 | 1 | 1 | |||||||||||||||||||
| Razem figura I | 3 | 1 | 2 | 0 | 119 | 107 | 13 | 13 | 13 | 27 | 15 | 19 | 2 | 5 | 0 | 4 | 8 | 1 | 6 | 1 | 2 | 124 | |
| 2 | 2 | 1 | 1 | 36 | 30 | 7 | 5 | 6 | 5 | 1 | 4 | 2 | 3 | 3 | 3 | 38 | |||||||
| 2m | 26 | 20 | 2 | 5 | 1 | 3 | 1 | 7 | 1 | 2 | 3 | 1 | 1 | 1 | 27 | ||||||||
| 2 obl | 1 | 1 | 1 | 1 | |||||||||||||||||||
| 2m obl | 5 | 5 | 5 | 5 | |||||||||||||||||||
| 2c | 1 | 1 | 5 | 5 | 5 | 6 | |||||||||||||||||
| Razem figura II | 3 | 1 | 1 | 1 | 73 | 56 | 9 | 10 | 7 | 8 | 8 | 11 | 0 | 3 | 2 | 6 | 9 | 0 | 9 | 0 | 1 | 77 | |
| 3 | 5 | 5 | 1 | 3 | 1 | 2 | 7 | ||||||||||||||||
| 3m | 6 | 6 | 2 | 2 | 1 | 1 | 1 | 7 | |||||||||||||||
| 3mc | 2 | 2 | 1 | 1 | 2 | ||||||||||||||||||
| Razem figura III | 13 | 13 | 1 | 3 | 5 | 1 | 3 | 3 | 16 | ||||||||||||||
| 4 | 2 | 2 | 1 | 1 | 2 | ||||||||||||||||||
| 4 obl | 1 | 1 | 1 | 1 | |||||||||||||||||||
| Razem figura IV | 3 | 3 | 2 | 1 | 3 | ||||||||||||||||||
| Razem dwuprzesłankowe | 6 | 2 | 3 | 1 | 208 | 179 | 23 | 26 | 25 | 38 | 23 | 34 | 2 | 8 | 2 | 10 | 17 | 1 | 15 | 1 | 6 | 220 | |
| sor3 | 2 | 1 | 1 | 35 | 34 | 8 | 10 | 4 | 5 | 3 | 2 | 2 | 1 | 1 | 38 | ||||||||
| sor3 obl | 5 | 5 | 2 | 2 | 1 | 5 | |||||||||||||||||
| sor3c | 1 | 1 | 1 | ||||||||||||||||||||
| Razem trójprzesłankowe | 2 | 1 | 1 | 41 | 39 | 10 | 10 | 6 | 5 | 4 | 2 | 2 | 2 | 1 | 44 | ||||||||
| sor4 | 1 | 1 | 10 | 10 | 1 | 5 | 1 | 3 | 1 | 12 | |||||||||||||
| sor4 obl | 1 | 1 | 1 | 1 | 2 | ||||||||||||||||||
| Razem czteroprzesłankowe | 1 | 1 | 11 | 11 | 1 | 5 | 1 | 3 | 1 | 2 | 14 | ||||||||||||
| sor5 | 3 | 3 | 2 | 1 | 1 | 4 | |||||||||||||||||
| Razem pięcioprzesłankowe | 3 | 3 | 2 | 1 | 1 | 4 | |||||||||||||||||
| sor9 | 1 | 1 | 1 | 1 | |||||||||||||||||||
| Razem dziewięcioprzesłankowe | 1 | 1 | 1 | 1 | |||||||||||||||||||
| wszystko | 9 | 2 | 2 | 4 | 1 | 278 | 244 | 36 | 44 | 32 | 49 | 28 | 42 | 2 | 11 | 2 | 15 | 17 | 1 | 15 | 1 | 14 | 301 |
Tabela 6. Te same dane, procenty
| figura | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| cons | 0 | 0 | 2 | 0 | |||||||||||||||||||
| cons obl | 0 | 0 | 21 | 1 | |||||||||||||||||||
| Razem cons | 0 | 0 | 2 | 21 | 1 | ||||||||||||||||||
| conv | 5 | 4 | 6 | 11 | 3 | 5 | 20 | 7 | 5 | ||||||||||||||
| Razem conv | 5 | 4 | 6 | 11 | 3 | 5 | 20 | 7 | 5 | ||||||||||||||
| Razem jednoprzesłankowe | 5 | 5 | 6 | 11 | 3 | 7 | 20 | 29 | 6 | ||||||||||||||
| 1 | 11 | 50 | 16 | 17 | 11 | 20 | 9 | 27 | 18 | 14 | 50 | 9 | 12 | 13 | 15 | ||||||||
| 1m | 11 | 25 | 21 | 22 | 17 | 9 | 28 | 22 | 21 | 29 | 50 | 36 | 13 | 12 | 7 | 100 | 14 | 20 | |||||
| 1 obl | 1 | 2 | 8 | 3 | 1 | ||||||||||||||||||
| 1m obl | 1 | 1 | 7 | 2 | 1 | ||||||||||||||||||
| 1c | 11 | 25 | 4 | 2 | 6 | 7 | 13 | 18 | 100 | 13 | 4 | ||||||||||||
| 1mc | 0 | 0 | 6 | 7 | 0 | ||||||||||||||||||
| Razem figura I | 33 | 50 | 50 | 0 | 43 | 44 | 36 | 30 | 41 | 55 | 54 | 45 | 100 | 45 | 0 | 27 | 47 | 100 | 40 | 100 | 14 | 41 | |
| 2 | 22 | 50 | 25 | 13 | 12 | 19 | 11 | 19 | 10 | 4 | 10 | 18 | 20 | 18 | 20 | 13 | |||||||
| 2m | 9 | 8 | 6 | 11 | 3 | 6 | 4 | 17 | 9 | 100 | 20 | 6 | 7 | 7 | 9 | ||||||||
| 2 obl | 0 | 0 | 4 | 0 | |||||||||||||||||||
| 2m obl | 2 | 2 | 18 | 2 | |||||||||||||||||||
| 2c | 11 | 100 | 2 | 0 | 29 | 33 | 2 | ||||||||||||||||
| Razem figura II | 33 | 50 | 25 | 100 | 26 | 23 | 25 | 23 | 22 | 16 | 29 | 26 | 0 | 27 | 100 | 40 | 53 | 0 | 60 | 0 | 7 | 26 | |
| 3 | 2 | 2 | 2 | 9 | 2 | 14 | 2 | ||||||||||||||||
| 3m | 2 | 2 | 5 | 6 | 2 | 2 | 7 | 2 | |||||||||||||||
| 3mc | 1 | 1 | 3 | 2 | 1 | ||||||||||||||||||
| Razem figura III | 5 | 5 | 3 | 7 | 16 | 2 | 7 | 21 | 5 | ||||||||||||||
| 4 | 1 | 1 | 2 | 2 | 1 | ||||||||||||||||||
| 4 obl | 0 | 0 | 2 | 0 | |||||||||||||||||||
| Razem figura IV | 1 | 1 | 4 | 2 | 1 | ||||||||||||||||||
| Razem dwuprzesłankowe | 67 | 100 | 75 | 100 | 75 | 73 | 64 | 59 | 78 | 78 | 82 | 81 | 100 | 73 | 100 | 67 | 100 | 100 | 100 | 100 | 43 | 73 | |
| sor3 | 22 | 50 | 25 | 13 | 14 | 22 | 23 | 13 | 10 | 11 | 5 | 18 | 7 | 7 | 13 | ||||||||
| sor3 obl | 2 | 2 | 6 | 6 | 4 | 2 | |||||||||||||||||
| sor3c | 0 | 0 | 7 | 0 | |||||||||||||||||||
| Razem trójprzesłankowe | 22 | 50 | 25 | 15 | 16 | 28 | 23 | 19 | 10 | 14 | 5 | 18 | 13 | 7 | 15 | ||||||||
| sor4 | 11 | 50 | 4 | 4 | 3 | 10 | 4 | 7 | 7 | 4 | |||||||||||||
| sor4 obl | 0 | 0 | 9 | 7 | 1 | ||||||||||||||||||
| Razem czteroprzesłankowe | 11 | 4 | 5 | 3 | 10 | 4 | 7 | 9 | 14 | 5 | |||||||||||||
| sor5 | 1 | 1 | 5 | 2 | 7 | 1 | |||||||||||||||||
| Razem pięcioprzesłankowe | 1 | 1 | 5 | 2 | 7 | 1 | |||||||||||||||||
| sor9 | 0 | 0 | 2 | 0 | |||||||||||||||||||
| Razem dziewięcioprzesłankowe | 0 | 0 | 2 | 0 | |||||||||||||||||||
| 100%= | 9 | 2 | 2 | 4 | 1 | 278 | 244 | 36 | 44 | 32 | 49 | 28 | 42 | 2 | 11 | 2 | 15 | 17 | 1 | 15 | 1 | 14 | 301 |
Tabela 7. Wszystkie reguły wg grup tekstów
| figura | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| reguły nazwowe o terminach prostych | 9 | 2 | 2 | 4 | 1 | 278 | 244 | 36 | 44 | 32 | 49 | 28 | 42 | 2 | 11 | 2 | 15 | 17 | 1 | 15 | 1 | 14 | 301 |
| reguły nazwowe o terminach złożonych | 1 | 1 | 27 | 21 | 1 | 2 | 10 | 2 | 5 | 1 | 5 | 1 | 1 | 28 | |||||||||
| reguły bez terminów nazwowych (wyłącznie zdaniowe) | 16 | 2 | 7 | 3 | 4 | 82 | 38 | 2 | 10 | 3 | 9 | 4 | 8 | 2 | 11 | 16 | 17 | 15 | 2 | 6 | 104 | ||
| reguły pozostałe | 2 | 1 | 1 | 33 | 19 | 4 | 4 | 3 | 6 | 2 | 11 | 3 | 3 | 35 | |||||||||
| Razem | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Tabela 8. Te same dane, procenty
| figura | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| reguły nazwowe o terminach prostych | 32 | 50 | 20 | 50 | 17 | 66 | 76 | 92 | 73 | 65 | 78 | 65 | 81 | 100 | 79 | 15 | 32 | 45 | 5 | 100 | 25 | 70 | 64 |
| reguły nazwowe o terminach złożonych | 4 | 13 | 6 | 7 | 3 | 3 | 20 | 3 | 12 | 7 | 11 | 3 | 25 | 6 | |||||||||
| reguły bez terminów nazwowych (wyłącznie zdaniowe) | 57 | 50 | 70 | 38 | 67 | 20 | 12 | 5 | 17 | 6 | 14 | 9 | 15 | 14 | 85 | 34 | 45 | 79 | 50 | 30 | 22 | ||
| reguły pozostałe | 7 | 10 | 17 | 8 | 6 | 7 | 8 | 5 | 14 | 4 | 23 | 8 | 16 | 7 | |||||||||
| 100%= | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Widać, że tradycyjna kolejność figur jest dobrze uzasadniona ich użytecznością: najczęstsza jest I (124 przypadki), po niej II (77), III (16) i IV (3). Zarazem ilość wystąpień fig. IV mieści się w granicach błędu, więc nieuwzględnienie jej przez Arystotelesa jest zupełnie zasadne.
Tradycyjnie przyjęło się, że w sylogizmach dwuprzesłankowych pierwsza jest tzw. przesłanka większa, zawierająca orzecznik konkluzji, druga zaś przesłanka mniejsza, zawierająca jej podmiot. W przypadku odwrotnej kolejności przesłanek mówi się o ich przestawieniu (metathesis). W fig. I mamy wyraźną przewagę reguł z przestawieniem przesłanek, tzn. 〈A_B, B_C ⊢ A_C〉 (60 przypadków) wobec 〈B_C, A_B ⊢ A_C〉 (45 przypadków). Odwrotnie dla fig. II: kolejność tradycyjna, tzn. 〈A_B, C_B ⊢ C_A〉 przeważa 38:27. W fig. III oba rodzaje mają po tyle samo przypadków, za mało jednak by coś na tej podstawie wnioskować (7:7).
Tryby skondycjonalizowane (sylogizmy hipotetyczne, różniące się od zwykłych tym, że wniosek ma charakter implikacji) są ciekawsze. W fig. I stosunek udziału 1c do 1mc, czyli 〈A_B ⊢ B_C → A_C〉 do 〈B_C ⊢ A_B → A_C〉 wynosi 11:1! W fig. II stosunek udziału 2c:2mc, czyli 〈A_B ⊢ C_B → A_C〉 do 〈A_B ⊢ C_B → C_A〉 wynosi już 6:0, ale pięć z tych sześciu przypadków pochodzi z jednego utworu (Dissoi logoi), nie można więc niczego ogólnego stąd wywnioskować.
Wśród reguł nazwowych rzuca się w oczy minimalny udział reguł innych niż dwuprzesłankowe reguły o terminach prostych (220): trójprzesłankowych reguł o terminach prostych jest już tylko 44, pozostałych (jedno-, cztero-, pięcio- i dziewięcioprzesłankowych razem): 37. Reguł o terminach złożonych (z ∩ lub ∪) jest tylko 28.
Jedynymi zależnościami między grupami tekstów, jakie da się jednoznacznie wychwycić, są proporcje reguł nazwowych do zdaniowych: w tekstach sokratyków ich procentowy udział wynosi odpowiednio 76 i 12, u eleatów 15 i 85, we fr. 53: 32 i 34, u innych filozofów 45:45 (Gorgiasz: 5 i 79, Dissoi logoi: 100 i 0), a w tekstach pozafilozoficznych: 32 i 57.
4. Reguły wg nazw zwyczajowych
Tabele poniższe ilustrują występowanie tych reguł logicznych, które mają swoje nazwy zwyczajowe: standardowych trybów sylogistycznych i niektórych reguł rachunku zdań.
Reguły nienazwane zostały podzielone wyczerpująco i rozłącznie na zdaniowe, nazwowe i mieszane. Do nazwowych (poza grupą 1.) zostały włączone wszystkie reguły nie zawierające funktorów zdaniowych oraz sylogizmy skondycjonalizowane (c) z grupy 3. Do zdaniowych zostały włączone wszystkie reguły nie zawierające funktorów nazwowych.
Tabela 9. Wg miejsc
| nazwa zwyczajowa | miejsca | ilość miejsc |
| conv. simplex e | 303 | 1 |
| Razem konwersje | 1 | |
| barbara | 18, 18, 23, 27, 41, 42, 42, 64, 68, 71, 74, 74, 79, 95, 95, 104, 105, 107, 107, 123, 123, 135, 140, 148 | 24 |
| barbara m | 18, 20, 22, 22, 27, 34, 46, 57, 60, 84, 98, 99, 101, 110, 112, 116, 120, 120, 123, 125, 125, 126, 140, 140, 141, 141, 146, 147, 153, 158, 159, 208 | 32 |
| barbara c | 38, 56, 58 | 3 |
| Razem barbara | 59 | |
| celarent | 45, 100, 126, 137 | 4 |
| celarent m | 14, 29, 37, 39, 45, 48, 64, 91, 96, 99, 116, 125, 129, 140, 141, 150 | 16 |
| celarent c | 16, 38, 38, 216 | 4 |
| Razem celarent | 24 | |
| darii | 137, 137 | 2 |
| darii c | 53 | 1 |
| Razem darii | 3 | |
| ferio c | 53 | 1 |
| Razem ferio | 1 | |
| Razem ważne tryby fig. I | 87 | |
| cesare | 26, 26, 33, 145, 156 | 5 |
| cesare m | 26, 26, 48, 50, 50, 67, 76, 76, 129, 152, 207, 207 | 12 |
| Razem cesare | 17 | |
| camestres | 14, 17, 18, 18, 26, 37, 53, 53, 53, 91, 96, 124, 125, 137, 144 | 15 |
| camestres m | 33, 53, 53, 92, 144, 156 | 6 |
| Razem camestres | 21 | |
| festino | 70, 88 | 2 |
| Razem festino | 2 | |
| baroco | 35 | 1 |
| baroco m | 47, 82, 101 | 3 |
| baroco c | 9 | 1 |
| Razem baroco | 5 | |
| Razem ważne tryby fig. II | 45 | |
| darapti | 74 | 1 |
| Razem darapti | 1 | |
| disamis m c | 32 | 1 |
| Razem disamis | 1 | |
| datisi | 87 | 1 |
| Razem datisi | 1 | |
| felapton | 88, 306 | 2 |
| Razem felapton | 2 | |
| bocardo m | 86 | 1 |
| Razem bocardo | 1 | |
| Razem ferison | 0 | |
| Razem ważne tryby fig. III | 6 | |
| Razem ważne tryby fig. IV | 0 | |
| Razem konwersje i ważne tryby fig. I–IV | 139 | |
| łańcuszniki redukowalne do ważnych trybów fig. I–IV | 5, 8, 15, 21, 22, 27, 27, 27, 27, 32, 36, 53, 54, 61, 62, 65, 69, 69, 72, 73, 77, 80, 93, 97, 99, 99, 102, 102, 121, 128, 131, 131, 132, 148, 155, 156 | 36 |
| „calerent” (paralogizm) | 103, 103 | 2 |
| ω-reguła (epagoge) | 133 | 1 |
| nienazwane nazwowe | 3, 14, 18, 18, 19, 25, 25, 25, 25, 28, 31, 31, 31, 31, 40, 40, 43, 43, 43, 46, 46, 46, 46, 46, 48, 48, 50, 51, 51, 51, 51, 51, 51, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 66, 67, 68, 76, 79, 79, 83, 85, 86, 93, 93, 94, 98, 107, 108, 108, 111, 112, 113, 114, 114, 115, 117, 118, 118, 118, 119, 119, 119, 119, 120, 120, 120, 120, 121, 121, 121, 121, 124, 124, 125, 125, 126, 126, 127, 127, 128, 129, 129, 129, 129, 133, 133, 133, 133, 133, 134, 134, 137, 137, 137, 137, 137, 137, 138, 138, 138, 138, 139, 140, 141, 141, 142, 143, 146, 148, 149, 151, 154, 156, 156, 157, 209, 217, 217, 217, 217, 217, 218, 218, 218, 219, 219, 219, 220, 220, 220, 220, 301, 301, 301, 301, 301, 301, 301, 302, 303, 304, 305, 305 | 155 |
| Razem reguły nazwowe | 333 | |
| reguła odrywania | 2, 51, 51, 53, 53, 53, 53, 53, 53, 66, 75, 130, 130, 149, 153, 202, 207, 207, 214, 307 | 20 |
| przechodniość implikacji | 11, 51, 122, 215 | 4 |
| Razem reguły czysto implikacyjne | 24 | |
| kontrapozycja | 201, 206 | 2 |
| słaba reg. dowodzenia niewprost | 1, 1, 1, 1, 6, 14, 16, 16, 32, 38, 38, 38, 49, 52, 53, 53, 53, 53, 53, 53, 53, 55, 63, 90, 136, 204, 205, 207, 207, 210, 213, 213, 213, 215 | 34 |
| słaby dowód niewprost | 24, 37, 43, 88, 99, 129, 130, 130, 131, 307 | 10 |
| mocna reg. dowodzenia niewprost | 4, 9, 12, 207, 211 | 5 |
| mocny dowód niewprost | 101 | 1 |
| Razem wnioskowania niewprost | 52 | |
| nienazwane zdaniowe | 1, 2, 10, 35, 44, 44, 45, 51, 53, 53, 53, 78, 108, 108, 136, 203, 212, 213, 213, 213, 213, 213, 214, 214, 215, 307, 307, 307, 307 | 29 |
| Razem reguły zdaniowe | 105 | |
| nienazwane mieszane | 3, 10, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 59, 66, 81, 89, 108, 119, 121, 130, 134, 138, 138, 140, 140, 146, 216, 216, 216 | 30 |
| Razem | 468 | |
Tabela 10. Konwersje i ważne tryby fig. I–IV wg grup tekstów
| nazwa zwyczajowa | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| conv. simplex e | 1 | 1 | |||||||||||||||||||||
| Razem konwersje | 1 | 1 | |||||||||||||||||||||
| barbara | 24 | 24 | 4 | 4 | 2 | 8 | 2 | 2 | 1 | 1 | 24 | ||||||||||||
| barbara m | 32 | 31 | 5 | 1 | 7 | 6 | 4 | 5 | 3 | 1 | 1 | 32 | |||||||||||
| barbara c | 3 | 3 | 1 | 2 | 3 | ||||||||||||||||||
| Razem barbara | 59 | 58 | 9 | 5 | 9 | 15 | 8 | 7 | 1 | 4 | 1 | 1 | 59 | ||||||||||
| celarent | 4 | 4 | 1 | 1 | 1 | 1 | 4 | ||||||||||||||||
| celarent m | 1 | 1 | 15 | 15 | 1 | 1 | 2 | 5 | 1 | 3 | 1 | 1 | 16 | ||||||||||
| celarent c | 1 | 1 | 3 | 2 | 2 | 1 | 1 | 4 | |||||||||||||||
| Razem celarent | 2 | 2 | 22 | 21 | 1 | 2 | 2 | 8 | 2 | 4 | 1 | 1 | 1 | 1 | 24 | ||||||||
| darii | 2 | 2 | 2 | 2 | |||||||||||||||||||
| darii c | 1 | 1 | 1 | ||||||||||||||||||||
| Razem darii | 3 | 2 | 2 | 1 | 3 | ||||||||||||||||||
| ferio c | 1 | 1 | 1 | ||||||||||||||||||||
| Razem ferio | 1 | 1 | 1 | ||||||||||||||||||||
| Razem ważne tryby fig. I | 2 | 2 | 85 | 81 | 10 | 7 | 11 | 23 | 12 | 11 | 2 | 5 | 2 | 2 | 1 | 1 | 87 | ||||||
| cesare | 5 | 5 | 2 | 2 | 1 | 5 | |||||||||||||||||
| cesare m | 12 | 10 | 2 | 3 | 1 | 3 | 1 | 2 | 12 | ||||||||||||||
| Razem cesare | 17 | 15 | 4 | 5 | 1 | 4 | 1 | 2 | 17 | ||||||||||||||
| camestres | 2 | 1 | 1 | 13 | 10 | 3 | 2 | 3 | 1 | 1 | 3 | 15 | |||||||||||
| camestres m | 6 | 4 | 2 | 1 | 1 | 2 | 6 | ||||||||||||||||
| Razem camestres | 2 | 1 | 1 | 19 | 14 | 3 | 2 | 2 | 4 | 1 | 2 | 5 | 21 | ||||||||||
| festino | 2 | 2 | 1 | 1 | 2 | ||||||||||||||||||
| Razem festino | 2 | 2 | 1 | 1 | 2 | ||||||||||||||||||
| baroco | 1 | 1 | 1 | 1 | |||||||||||||||||||
| baroco m | 3 | 3 | 1 | 1 | 1 | 3 | |||||||||||||||||
| baroco c | 1 | 1 | 1 | ||||||||||||||||||||
| Razem baroco | 1 | 1 | 4 | 4 | 1 | 2 | 1 | 5 | |||||||||||||||
| Razem ważne tryby fig. II | 3 | 1 | 1 | 1 | 42 | 35 | 7 | 8 | 4 | 6 | 2 | 7 | 1 | 2 | 5 | 45 | |||||||
| darapti | 1 | 1 | 1 | 1 | |||||||||||||||||||
| Razem darapti | 1 | 1 | 1 | 1 | |||||||||||||||||||
| disamis m c | 1 | 1 | 1 | 1 | |||||||||||||||||||
| Razem disamis | 1 | 1 | 1 | 1 | |||||||||||||||||||
| datisi | 1 | 1 | 1 | 1 | |||||||||||||||||||
| Razem datisi | 1 | 1 | 1 | 1 | |||||||||||||||||||
| felapton | 1 | 1 | 1 | 1 | 2 | ||||||||||||||||||
| Razem felapton | 1 | 1 | 1 | 1 | 2 | ||||||||||||||||||
| bocardo m | 1 | 1 | 1 | 1 | |||||||||||||||||||
| Razem bocardo | 1 | 1 | 1 | 1 | |||||||||||||||||||
| Razem ferison | 0 | ||||||||||||||||||||||
| Razem ważne tryby fig. III | 5 | 5 | 1 | 1 | 3 | 1 | 6 | ||||||||||||||||
| Razem ważne tryby fig. IV | 0 | ||||||||||||||||||||||
| wszystko | 5 | 0 | 1 | 3 | 1 | 132 | 121 | 18 | 16 | 18 | 29 | 14 | 18 | 2 | 6 | 2 | 7 | 2 | 1 | 0 | 1 | 2 | 139 |
Tabela 11. Te same dane, procenty
| nazwa zwyczajowa | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| conv. simplex e | 0 | 0 | 50 | 1 | |||||||||||||||||||
| Razem konwersje | 0 | 0 | 50 | 1 | |||||||||||||||||||
| barbara | 18 | 20 | 22 | 25 | 11 | 28 | 14 | 11 | 50 | 17 | 17 | ||||||||||||
| barbara m | 24 | 26 | 28 | 6 | 39 | 21 | 29 | 28 | 50 | 50 | 100 | 23 | |||||||||||
| barbara c | 2 | 2 | 3 | 14 | 2 | ||||||||||||||||||
| Razem barbara | 45 | 48 | 50 | 31 | 50 | 52 | 57 | 39 | 50 | 67 | 50 | 100 | 42 | ||||||||||
| celarent | 3 | 3 | 6 | 3 | 7 | 6 | 3 | ||||||||||||||||
| celarent m | 20 | 33 | 11 | 12 | 6 | 6 | 11 | 17 | 7 | 17 | 50 | 17 | 12 | ||||||||||
| celarent c | 20 | 33 | 2 | 2 | 7 | 50 | 100 | 3 | |||||||||||||||
| Razem celarent | 40 | 67 | 17 | 17 | 6 | 13 | 11 | 28 | 14 | 22 | 50 | 17 | 50 | 100 | 17 | ||||||||
| darii | 2 | 2 | 14 | 1 | |||||||||||||||||||
| darii c | 1 | 0 | 14 | 1 | |||||||||||||||||||
| Razem darii | 2 | 2 | 14 | 14 | 2 | ||||||||||||||||||
| ferio c | 1 | 0 | 14 | 1 | |||||||||||||||||||
| Razem ferio | 1 | 0 | 14 | 1 | |||||||||||||||||||
| Razem ważne tryby fig. I | 40 | 67 | 64 | 67 | 56 | 44 | 61 | 79 | 86 | 61 | 100 | 83 | 29 | 100 | 100 | 100 | 63 | ||||||
| cesare | 4 | 4 | 11 | 13 | 6 | 4 | |||||||||||||||||
| cesare m | 9 | 8 | 11 | 19 | 7 | 17 | 17 | 100 | 9 | ||||||||||||||
| Razem cesare | 13 | 12 | 22 | 31 | 7 | 22 | 17 | 100 | 12 | ||||||||||||||
| camestres | 40 | 100 | 33 | 10 | 8 | 17 | 11 | 10 | 7 | 6 | 43 | 11 | |||||||||||
| camestres m | 5 | 3 | 13 | 3 | 6 | 29 | 4 | ||||||||||||||||
| Razem camestres | 40 | 100 | 33 | 14 | 12 | 17 | 13 | 11 | 14 | 7 | 11 | 71 | 15 | ||||||||||
| festino | 2 | 2 | 6 | 6 | 1 | ||||||||||||||||||
| Razem festino | 2 | 2 | 6 | 6 | 1 | ||||||||||||||||||
| baroco | 1 | 1 | 3 | 1 | |||||||||||||||||||
| baroco m | 2 | 2 | 6 | 3 | 6 | 2 | |||||||||||||||||
| baroco c | 20 | 100 | 0 | 0 | 1 | ||||||||||||||||||
| Razem baroco | 20 | 100 | 3 | 3 | 6 | 7 | 6 | 4 | |||||||||||||||
| Razem ważne tryby fig. II | 60 | 100 | 33 | 100 | 32 | 29 | 39 | 50 | 22 | 21 | 14 | 39 | 17 | 100 | 71 | 32 | |||||||
| darapti | 1 | 1 | 6 | 1 | |||||||||||||||||||
| Razem darapti | 1 | 1 | 6 | 1 | |||||||||||||||||||
| disamis m c | 1 | 1 | 6 | 1 | |||||||||||||||||||
| Razem disamis | 1 | 1 | 6 | 1 | |||||||||||||||||||
| datisi | 1 | 1 | 6 | 1 | |||||||||||||||||||
| Razem datisi | 1 | 1 | 6 | 1 | |||||||||||||||||||
| felapton | 1 | 1 | 6 | 50 | 1 | ||||||||||||||||||
| Razem felapton | 1 | 1 | 6 | 50 | 1 | ||||||||||||||||||
| bocardo m | 1 | 1 | 6 | 1 | |||||||||||||||||||
| Razem bocardo | 1 | 1 | 6 | 1 | |||||||||||||||||||
| Razem ferison | 0 | 0 | 0 | ||||||||||||||||||||
| Razem ważne tryby fig. III | 4 | 4 | 6 | 6 | 17 | 50 | 4 | ||||||||||||||||
| Razem ważne tryby fig. IV | 0 | 0 | 0 | ||||||||||||||||||||
| 100%= | 5 | 0 | 1 | 3 | 1 | 132 | 121 | 18 | 16 | 18 | 29 | 14 | 18 | 2 | 6 | 2 | 7 | 2 | 1 | 0 | 1 | 2 | 139 |
Tabela 12. Wszystkie reguły nazwowe wg grup tekstów
| nazwa zwyczajowa | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| konwersje i ważne tryby fig. I–IV | 5 | 1 | 3 | 1 | 132 | 121 | 18 | 16 | 18 | 29 | 14 | 18 | 2 | 6 | 2 | 7 | 2 | 1 | 1 | 2 | 139 | ||
| łańcuszniki redukowalne do trybów fig. I–IV | 3 | 2 | 1 | 33 | 32 | 7 | 9 | 1 | 7 | 4 | 2 | 2 | 1 | 36 | |||||||||
| „calerent” (paralogizm) | 2 | 2 | 2 | 2 | |||||||||||||||||||
| ω-reguła (epagoge) | 1 | 1 | 1 | 1 | |||||||||||||||||||
| nienazwane nazwowe | 2 | 1 | 1 | 141 | 113 | 12 | 22 | 24 | 14 | 15 | 22 | 4 | 12 | 16 | 15 | 1 | 12 | 155 | |||||
| wszystko | 10 | 2 | 2 | 5 | 1 | 309 | 269 | 37 | 48 | 43 | 52 | 33 | 42 | 2 | 12 | 2 | 20 | 18 | 1 | 15 | 2 | 14 | 333 |
Tabela 13. Te same dane, procenty
| nazwa zwyczajowa | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| konwersje i ważne tryby fig. I–IV | 50 | 50 | 60 | 100 | 43 | 45 | 49 | 33 | 42 | 56 | 42 | 43 | 100 | 50 | 100 | 35 | 11 | 100 | 50 | 14 | 42 | ||
| łańcuszniki redukowalne do trybów fig. I–IV | 30 | 100 | 20 | 11 | 12 | 19 | 19 | 2 | 13 | 12 | 5 | 17 | 5 | 11 | |||||||||
| „calerent” (paralogizm) | 1 | 1 | 4 | 1 | |||||||||||||||||||
| ω-reguła (epagoge) | 0 | 0 | 2 | 0 | |||||||||||||||||||
| nienazwane nazwowe | 20 | 50 | 20 | 46 | 42 | 32 | 46 | 56 | 27 | 45 | 52 | 33 | 60 | 89 | 100 | 50 | 86 | 47 | |||||
| 100%= | 10 | 2 | 2 | 5 | 1 | 309 | 269 | 37 | 48 | 43 | 52 | 33 | 42 | 2 | 12 | 2 | 20 | 18 | 1 | 15 | 2 | 14 | 333 |
Tabela 14. Reguły zdaniowe wg grup tekstów
| nazwa zwyczajowa | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| reguła odrywania | 1 | 1 | 18 | 8 | 3 | 1 | 2 | 2 | 3 | 6 | 1 | 1 | 1 | 20 | |||||||||
| przechodniość implikacji | 1 | 1 | 3 | 2 | 1 | 1 | 1 | 1 | 4 | ||||||||||||||
| Razem reguły czysto implikacyjne | 2 | 1 | 1 | 21 | 10 | 3 | 1 | 1 | 3 | 2 | 3 | 6 | 2 | 2 | 1 | 24 | |||||||
| kontrapozycja | 2 | 2 | 2 | ||||||||||||||||||||
| słaba reg. dowodzenia niewprost | 8 | 1 | 4 | 3 | 26 | 10 | 1 | 1 | 1 | 3 | 3 | 1 | 4 | 7 | 5 | 4 | 1 | 34 | |||||
| słaby dowód niewprost | 9 | 9 | 1 | 4 | 1 | 2 | 1 | 1 | 10 | ||||||||||||||
| mocna reg. dowodzenia niewprost | 3 | 1 | 2 | 2 | 1 | 1 | 1 | 5 | |||||||||||||||
| mocny dowód niewprost | 1 | 1 | 1 | 1 | |||||||||||||||||||
| Razem wnioskowania niewprost | 11 | 2 | 4 | 3 | 2 | 40 | 20 | 2 | 5 | 2 | 6 | 3 | 2 | 7 | 7 | 6 | 4 | 2 | 1 | 52 | |||
| nienazwane zdaniowe | 3 | 2 | 1 | 22 | 9 | 2 | 3 | 4 | 1 | 3 | 9 | 9 | 4 | 29 | |||||||||
| wszystko | 16 | 2 | 7 | 3 | 4 | 83 | 39 | 2 | 10 | 3 | 9 | 4 | 9 | 0 | 2 | 11 | 16 | 17 | 15 | 0 | 2 | 6 | 105 |
Tabela 15. Te same dane, procenty
| nazwa zwyczajowa | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| reguła odrywania | 6 | 14 | 22 | 21 | 30 | 25 | 22 | 100 | 27 | 38 | 6 | 7 | 17 | 19 | |||||||||
| przechodniość implikacji | 6 | 25 | 4 | 5 | 33 | 11 | 6 | 7 | 4 | ||||||||||||||
| Razem reguły czysto implikacyjne | 13 | 14 | 25 | 25 | 26 | 30 | 33 | 25 | 33 | 100 | 27 | 38 | 12 | 13 | 17 | 23 | |||||||
| kontrapozycja | 2 | 18 | 2 | ||||||||||||||||||||
| słaba reg. dowodzenia niewprost | 50 | 50 | 57 | 100 | 31 | 26 | 50 | 10 | 33 | 33 | 75 | 11 | 36 | 44 | 29 | 27 | 50 | 32 | |||||
| słaby dowód niewprost | 11 | 23 | 50 | 40 | 33 | 22 | 11 | 17 | 10 | ||||||||||||||
| mocna reg. dowodzenia niewprost | 19 | 50 | 50 | 2 | 0 | 9 | 6 | 50 | 5 | ||||||||||||||
| mocny dowód niewprost | 1 | 3 | 11 | 1 | |||||||||||||||||||
| Razem wnioskowania niewprost | 69 | 100 | 57 | 100 | 50 | 48 | 51 | 100 | 50 | 67 | 67 | 75 | 22 | 64 | 44 | 35 | 27 | 100 | 17 | 50 | |||
| nienazwane zdaniowe | 19 | 29 | 25 | 27 | 23 | 20 | 33 | 44 | 9 | 19 | 53 | 60 | 67 | 28 | |||||||||
| 100%= | 16 | 2 | 7 | 3 | 4 | 83 | 39 | 2 | 10 | 3 | 9 | 4 | 9 | 0 | 2 | 11 | 16 | 17 | 15 | 0 | 2 | 6 | 105 |
Tabela 16. Wszystkie reguły wg grup tekstów
| nazwa zwyczajowa | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| reguły nazwowe | 10 | 2 | 2 | 5 | 1 | 309 | 269 | 37 | 48 | 43 | 52 | 33 | 42 | 2 | 12 | 2 | 20 | 18 | 1 | 15 | 2 | 14 | 333 |
| reguły zdaniowe | 16 | 2 | 7 | 3 | 4 | 83 | 39 | 2 | 10 | 3 | 9 | 4 | 9 | 2 | 11 | 16 | 17 | 15 | 2 | 6 | 105 | ||
| nienazwane mieszane | 2 | 1 | 1 | 28 | 14 | 2 | 3 | 2 | 6 | 1 | 11 | 3 | 3 | 30 | |||||||||
| wszystko | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Tabela 17. Te same dane, procenty
| nazwa zwyczajowa | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| reguły nazwowe | 36 | 50 | 20 | 63 | 17 | 74 | 84 | 95 | 80 | 88 | 83 | 77 | 81 | 100 | 86 | 15 | 43 | 47 | 5 | 100 | 50 | 70 | 71 |
| reguły zdaniowe | 57 | 50 | 70 | 38 | 67 | 20 | 12 | 5 | 17 | 6 | 14 | 9 | 17 | 14 | 85 | 34 | 45 | 79 | 50 | 30 | 22 | ||
| nienazwane mieszane | 7 | 10 | 17 | 7 | 4 | 3 | 6 | 3 | 14 | 2 | 23 | 8 | 16 | 6 | |||||||||
| 100%= | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Tabele te pozwalają na przeprowadzenie podziału wśród znalezionych reguł pod względem ich sensu logicznego.
Po pierwsze, większość wszystkich reguł stanowią reguły nazwowe, czyli sylogizmy (71% wszędzie, 84% u sokratyków). Spośród reguł nazwowych większość stanowią tryby posługujące się czterema klasycznymi funktorami (⊆, ∥, ∦, ⊈, czyli scholastyczne a, e, i, o; odpowiednio: 53% i 57%) — na tryby używające przynajmniej jednego z pozostałych pięciu funktorów nazwowych (lub funktora specyficznego) przypada 47% (42% u sokratyków). Spośród tych pierwszych tylko 21% to tryby o ilości przesłanek różnej od dwóch. Tak więc, wprawdzie klasyczne, Arystotelesowe sylogizmy dwuprzesłankowe (bez figury IV) stanowią tylko odpowiednio 29% (37%) wszystkich znalezionych reguł, to stanowią one największą i najjednorodniejszą grupę, mogą być więc śmiało nazwane logiką par excellence jeszcze należy, że ważne tryby fig. I (sylogizmy doskonałe Arystotelesa) stanowią 63% (67%) wszystkich, zaś sam tryb „barbara” — 42% (48%).
Należy zrewidować wcześniejsze uwagi o proporcji trybów standardowych do trybów z przestawieniem przesłanek. Widać bowiem niezwykle wyraźnie, że w fig. I, gdzie stosunek ten wynosił 45:60, podczas gdy dla trybu „barbara” wynosi on 24:32 (3:4, a więc tyle samo), to dla trybu „celarent” aż 4:16 (1:4). W fig. II, gdzie ogólnie było 38:27, dla trybu „cesare” jest 5:12 (1,7:4), a dla „camestres” 15:6 (4:1,6). Można więc podsumować, że niezależnie od układu terminów, proporcja układu aee (⊆∥∥) do eae (∥⊆∥) wynosi 43:15, czyli 4:1,4.
Z logiki czysto zdaniowej, która obejmuje 22% (12% u sokratyków) wszystkich reguł, należy zwrócić uwagę przede wszystkim na logikę implikacyjno-negacyjną, która stanowi 72% (77%). Mniejsza jej część to rachunek czystej implikacji: reguła odrywania to odpowiednio 19% i 21%, a przechodniość implikacji 4% (5%) wszystkich reguł zdaniowych. Reszta, a zarazem połowa wszystkich reguł zdaniowych to różne formy dowodzenia niewprost. Składają się na nie: kontrapozycja (np. α→β ⊢ ~β→~α), reguła dowodzenia niewprost (np. α→β, ~β ⊢ ~α), czy wreszcie dowód niewprost (np. (α, Γ ⊢ β), ~β |- ~α); w regułach tych miejsce może zmieniać negacja, można je też rozbudowywać o przechodniość implikacji (np. α→β, β→~γ, γ ⊢ ~α). Wśród różnych form dowodzenia niewprost ważniejszy od podziału na kontrapozycję, regułę dowodzenia niewprost i dowody niewprost jest podział na dowodzenie słabe (formuły zanegowanej) i mocne (formuły pozytywnej). Stosunek ilości reguł obalających (z negacją we wniosku) do reguł mocnych wynosi 46:6 (odpowiednio 19:1 u sokratyków).
5. Ilość przesłanek w regułach
Tabela 18. Wg miejsc
| ilość przesłanek | miejsca | ilość miejsc |
| 1 | 2, 9, 16, 25, 25, 32, 38, 38, 38, 43, 44, 48, 48, 51, 53, 53, 53, 53, 53, 53, 56, 58, 121, 124, 126, 128, 133, 134, 138, 157, 201, 206, 216, 218, 218, 219, 219, 220, 220, 220, 220, 301, 301, 303, 305 | 45 |
| 2 | 1, 1, 1, 1, 2, 3, 4, 6, 9, 10, 12, 14, 14, 14, 14, 16, 16, 17, 18, 18, 18, 18, 18, 18, 18, 20, 22, 22, 23, 24, 26, 26, 26, 26, 26, 27, 27, 29, 31, 31, 31, 32, 33, 33, 34, 35, 35, 37, 37, 37, 38, 38, 38, 39, 40, 41, 42, 42, 43, 43, 43, 45, 45, 45, 46, 46, 46, 46, 47, 48, 48, 49, 50, 50, 50, 51, 51, 51, 51, 51, 51, 51, 51, 51, 52, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 55, 57, 60, 63, 64, 64, 66, 66, 66, 67, 67, 68, 68, 70, 71, 74, 74, 74, 75, 76, 76, 78, 79, 79, 79, 82, 83, 84, 85, 86, 86, 87, 88, 88, 88, 90, 91, 91, 92, 95, 95, 96, 96, 98, 98, 99, 99, 99, 100, 101, 101, 101, 103, 103, 104, 105, 107, 107, 107, 108, 108, 108, 108, 110, 111, 112, 114, 115, 116, 116, 117, 118, 119, 120, 120, 120, 120, 123, 123, 123, 124, 125, 125, 125, 125, 125, 126, 126, 127, 127, 129, 129, 129, 129, 129, 129, 130, 130, 130, 130, 130, 131, 133, 133, 133, 134, 135, 137, 137, 137, 137, 137, 137, 137, 137, 137, 138, 138, 139, 140, 140, 140, 140, 140, 141, 141, 141, 141, 142, 143, 144, 144, 145, 146, 146, 147, 148, 148, 149, 149, 150, 152, 153, 153, 156, 156, 156, 158, 159, 202, 205, 207, 207, 207, 207, 207, 207, 208, 211, 214, 215, 215, 217, 217, 217, 217, 217, 218, 219, 301, 301, 301, 301, 302, 306, 307, 307 | 292 |
| 3 | 3, 8, 10, 15, 19, 21, 25, 25, 27, 27, 27, 27, 31, 32, 40, 44, 46, 53, 53, 53, 53, 53, 53, 53, 53, 54, 61, 65, 69, 72, 73, 76, 81, 93, 93, 94, 102, 108, 113, 114, 118, 118, 119, 119, 119, 119, 120, 121, 121, 121, 122, 124, 125, 128, 129, 131, 131, 133, 136, 136, 137, 138, 138, 138, 140, 140, 146, 148, 155, 156, 156, 203, 204, 207, 209, 210, 213, 214, 215, 216, 216, 216, 301, 307 | 84 |
| 4 | 5, 11, 22, 28, 36, 46, 53, 53, 62, 69, 80, 89, 97, 99, 99, 112, 120, 126, 141, 151, 154, 213, 303, 305, 307, 307, 307 | 27 |
| 5 | 1, 59, 93, 102, 121, 121, 132, 212, 213, 304 | 10 |
| 6 | 53, 213 | 2 |
| 7 | 134, 213, 214 | 3 |
| 8 | 213 | 1 |
| 9 | 77 | 1 |
| 10 | 213 | 1 |
| 11 | 213 | 1 |
| ω | 133 | 1 |
| Razem | 468 | |
Tabela 19. Wg grup tekstów
| ilość przesłanek | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| 1 | 3 | 1 | 1 | 1 | 38 | 21 | 3 | 5 | 2 | 3 | 3 | 5 | 2 | 6 | 9 | 1 | 8 | 4 | 45 | ||||
| 2 | 18 | 2 | 7 | 6 | 3 | 266 | 216 | 24 | 35 | 30 | 46 | 29 | 40 | 2 | 10 | 8 | 30 | 12 | 3 | 7 | 2 | 8 | 292 |
| 3 | 4 | 1 | 1 | 1 | 1 | 78 | 59 | 10 | 14 | 13 | 7 | 9 | 4 | 2 | 3 | 8 | 8 | 6 | 2 | 2 | 84 | ||
| 4 | 2 | 1 | 1 | 20 | 17 | 2 | 1 | 2 | 6 | 1 | 3 | 2 | 2 | 1 | 1 | 5 | 27 | ||||||
| 5 | 1 | 1 | 8 | 6 | 2 | 2 | 1 | 1 | 2 | 2 | 1 | 10 | |||||||||||
| 6 | 2 | 1 | 1 | 1 | 2 | ||||||||||||||||||
| 7 | 3 | 1 | 1 | 2 | 2 | 3 | |||||||||||||||||
| 8 | 1 | 1 | 1 | 1 | |||||||||||||||||||
| 9 | 1 | 1 | 1 | 1 | |||||||||||||||||||
| 10 | 1 | 1 | 1 | 1 | |||||||||||||||||||
| 11 | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ω | 1 | 1 | 1 | 1 | |||||||||||||||||||
| wszystko | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Tabela 20. Te same dane, procenty
| ilość przesłanek | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| 1 | 11 | 10 | 13 | 17 | 9,0 | 6,5 | 8 | 8 | 4 | 5 | 7 | 10 | 15 | 13 | 24 | 5 | 53 | 20 | 9,6 | ||||
| 2 | 64 | 50 | 70 | 75 | 50 | 63,3 | 67,1 | 62 | 58 | 61 | 73 | 67 | 77 | 100 | 71 | 62 | 64 | 32 | 16 | 47 | 50 | 40 | 62,4 |
| 3 | 14 | 25 | 10 | 13 | 17 | 18,6 | 18,3 | 26 | 23 | 27 | 11 | 21 | 8 | 14 | 23 | 17 | 21 | 32 | 50 | 10 | 17,9 | ||
| 4 | 7 | 25 | 17 | 4,8 | 5,3 | 5 | 2 | 4 | 10 | 2 | 6 | 14 | 4 | 3 | 5 | 25 | 5,8 | ||||||
| 5 | 4 | 10 | 1,9 | 1,9 | 3 | 4 | 2 | 2 | 5 | 11 | 5 | 2,1 | |||||||||||
| 6 | 0,5 | 2 | 3 | 5 | 0,4 | ||||||||||||||||||
| 7 | 0,7 | 0,3 | 2 | 5 | 11 | 0,6 | |||||||||||||||||
| 8 | 0,2 | 3 | 5 | 0,2 | |||||||||||||||||||
| 9 | 0,2 | 0,3 | 2 | 0,2 | |||||||||||||||||||
| 10 | 0,2 | 3 | 5 | 0,2 | |||||||||||||||||||
| 11 | 0,2 | 3 | 5 | 0,2 | |||||||||||||||||||
| ω | 0,2 | 0,3 | 2 | 0,2 | |||||||||||||||||||
| 100%= | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Jak widać, reguły dwuprzesłankowe stanowią prawie 2/3 ogólnej liczby reguł (62,4% dla wszystkich, 67,1% dla sokratyków). Poza regułami trójprzesłankowymi (17,9% i 18,3% odpowiednio), jednoprzesłankowymi (9,6% i 6,5%) oraz czteroprzesłankowymi (5,8% i 5,3%), żaden inny typ nie przekracza progu jednego procenta (w sumie mają 2,1% i 2,8%).
6. Zestawy funktorów w regułach
Tabela 21. Wg miejsc
| funktory | miejsca | ilość miejsc |
| ⊆ | 5, 15, 18, 18, 18, 20, 21, 22, 22, 22, 23, 27, 27, 27, 27, 27, 27, 32, 34, 36, 41, 42, 42, 46, 54, 57, 60, 61, 62, 64, 68, 69, 69, 71, 72, 73, 74, 74, 77, 79, 80, 84, 95, 95, 97, 98, 99, 99, 101, 102, 102, 104, 105, 107, 107, 110, 112, 116, 120, 120, 121, 123, 123, 123, 125, 125, 126, 132, 135, 140, 140, 140, 141, 141, 146, 147, 148, 148, 153, 155, 156, 158, 159, 208 | 84 |
| ⊆ = | 18, 18, 25, 25, 79, 114, 120, 120, 121, 127, 129, 129, 133, 133, 148, 149, 217, 217, 217, 218, 219, 304 | 22 |
| ⊆ = ¬ | 25, 114 | 2 |
| ⊆ = ∥ | 46 | 1 |
| ⊆ = ∥ sp | 40 | 1 |
| ⊆ = ∩ | 118, 138 | 2 |
| ⊆ = ∪ | 120 | 1 |
| ⊆ = → | 51, 218, 218, 219, 219, 220, 220, 220, 220 | 9 |
| ⊆ = sp | 19, 119, 137, 137, 137, 305 | 6 |
| ⊆ ∦ | 74, 87, 137, 137 | 4 |
| ⊆ ∦ ¬ ⊈ sp | 86 | 1 |
| ⊆ ∦ ∥ ⊈ | 128 | 1 |
| ⊆ ∦ ∥ ∪ → ~ | 53 | 1 |
| ⊆ ∦ ∥ → | 53 | 1 |
| ⊆ ∦ ∥ → ~ | 53 | 1 |
| ⊆ ∦ → | 32, 53 | 2 |
| ⊆ ∦ sp | 137, 137, 137 | 3 |
| ⊆ ¬ | 48, 79 | 2 |
| ⊆ ¬ ∥ | 25, 40, 46, 48, 53, 53, 53, 53, 67, 93, 94, 98, 113, 121, 126, 128, 133, 141, 157, 303 | 20 |
| ⊆ ¬ ∥ ∩ | 124 | 1 |
| ⊆ ¬ ∥ ∩ → ∧ | 59 | 1 |
| ⊆ ∥ | 8, 14, 14, 17, 18, 18, 26, 26, 26, 26, 26, 29, 33, 33, 37, 37, 39, 45, 45, 48, 48, 50, 50, 53, 53, 53, 53, 53, 64, 65, 67, 76, 76, 91, 91, 92, 93, 96, 96, 99, 99, 100, 103, 103, 116, 124, 125, 125, 126, 129, 129, 131, 131, 137, 137, 140, 141, 144, 144, 145, 150, 152, 156, 156, 207, 207 | 66 |
| ⊆ ∥ ⊈ | 88, 306 | 2 |
| ⊆ ∥ ≠ | 46, 111, 117, 142, 302 | 5 |
| ⊆ ∥ ∩ | 14, 112 | 2 |
| ⊆ ∥ ∩ ∪ | 53, 53, 53 | 3 |
| ⊆ ∥ ∪ | 53, 76, 118, 120, 125, 156, 209 | 7 |
| ⊆ ∥ ∪ → | 216, 216 | 2 |
| ⊆ ∥ ∪ sp | 53, 119 | 2 |
| ⊆ ∥ → | 16, 38, 38, 53, 216 | 5 |
| ⊆ ∥ → ~ ∧ | 216 | 1 |
| ⊆ ∥ sp | 126 | 1 |
| ⊆ ⊈ | 35, 47, 82, 86, 101 | 5 |
| ⊆ ⊈ ≠ | 83, 85, 143 | 3 |
| ⊆ ⊈ → | 9 | 1 |
| ⊆ ⊈ → ~ | 81 | 1 |
| ⊆ ⊈ ⊥ | 89 | 1 |
| ⊆ ∩ | 28, 107, 121, 138, 140, 154 | 6 |
| ⊆ ∩ ∪ | 118 | 1 |
| ⊆ ∩ → | 138, 138 | 2 |
| ⊆ ∩ sp | 138, 138 | 2 |
| ⊆ → | 38, 53, 56, 58, 66, 119, 121, 146 | 8 |
| ⊆ → sp | 140, 140 | 2 |
| ⊆ ∧ | 130 | 1 |
| ⊆ sp | 31, 31, 31, 31, 66, 68, 119, 119, 139, 141, 151, 305 | 12 |
| = | 3, 43, 51, 51, 51, 121, 129, 133, 133, 133, 134, 134, 217, 217, 301, 301, 301 | 17 |
| = ¬ | 43, 108, 108 | 3 |
| = ¬ ⊈ | 43 | 1 |
| = ∥ | 125, 127, 129, 146, 301, 301 | 6 |
| = ≠ | 51 | 1 |
| = ≠ ⊻ | 3 | 1 |
| = ∩ ∪ → | 134 | 1 |
| = → | 108 | 1 |
| = → ∧ sp | 10 | 1 |
| = sp | 301, 301 | 2 |
| ∦ ¬ ∥ ∪ → ⊻ | 53 | 1 |
| ∦ ∥ ⊈ | 70, 88 | 2 |
| ∦ ∥ ⊈ → | 53 | 1 |
| ∦ ∥ ≠ | 115, 156 | 2 |
| ∦ ∥ ∩ ∪ → | 53 | 1 |
| ∦ ∥ ∪ → | 53 | 1 |
| ∦ ∥ ∪ → ~ ∧ | 53 | 1 |
| ¬ ∥ | 46, 46, 50, 51, 53, 53, 53, 93 | 8 |
| ¬ ∥ ∩ | 124 | 1 |
| ∥ | 303 | 1 |
| ⊈ → ~ | 53, 53 | 2 |
| ≠ → ~ | 53 | 1 |
| → | 2, 11, 51, 51, 51, 53, 53, 53, 53, 53, 53, 66, 75, 122, 130, 130, 149, 153, 202, 207, 207, 214, 215, 307 | 24 |
| → ~ | 1, 1, 1, 1, 4, 6, 9, 12, 14, 16, 16, 32, 38, 38, 38, 45, 49, 52, 53, 53, 53, 53, 53, 53, 53, 55, 63, 90, 136, 201, 204, 205, 206, 207, 207, 207, 210, 211, 213, 213, 213, 215 | 42 |
| → ~ ∧ | 51, 53, 203 | 3 |
| → ~ ∧ ∨ | 53 | 1 |
| → ~ ∨ | 2, 213, 213, 213, 213, 213, 214, 214 | 8 |
| → ~ ∨ ⊻ ↔ | 44 | 1 |
| → ~ ⊻ | 136 | 1 |
| → ∧ | 10, 53, 78, 108, 215, 307, 307, 307, 307 | 9 |
| → ∨ | 212 | 1 |
| ~ | 24, 37, 43, 88, 99, 101, 129, 130, 130, 131, 307 | 11 |
| ~ ∧ ∨ ⊻ ↔ | 44 | 1 |
| ~ ∨ | 1, 108 | 2 |
| ~ ⊻ | 35 | 1 |
| Razem | 468 | |
Tabela 22. Wg grup tekstów
| funktory | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| ⊆ | 2 | 1 | 1 | 82 | 81 | 16 | 10 | 10 | 20 | 9 | 9 | 1 | 6 | 1 | 1 | 84 | |||||||
| ⊆ = | 21 | 16 | 4 | 5 | 3 | 2 | 2 | 5 | 5 | 1 | 22 | ||||||||||||
| ⊆ = ¬ | 2 | 2 | 1 | 1 | 2 | ||||||||||||||||||
| ⊆ = ∥ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ = ∥ sp | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ = ∩ | 2 | 2 | 1 | 1 | 2 | ||||||||||||||||||
| ⊆ = ∪ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ = → | 9 | 1 | 1 | 8 | 8 | 9 | |||||||||||||||||
| ⊆ = sp | 5 | 5 | 1 | 1 | 3 | 1 | 6 | ||||||||||||||||
| ⊆ ∦ | 4 | 4 | 1 | 1 | 2 | 4 | |||||||||||||||||
| ⊆ ∦ ¬ ⊈ sp | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ ∦ ∥ ⊈ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ ∦ ∥ ∪ → ~ | 1 | 1 | 1 | ||||||||||||||||||||
| ⊆ ∦ ∥ → | 1 | 1 | 1 | ||||||||||||||||||||
| ⊆ ∦ ∥ → ~ | 1 | 1 | 1 | ||||||||||||||||||||
| ⊆ ∦ → | 2 | 1 | 1 | 1 | 2 | ||||||||||||||||||
| ⊆ ∦ sp | 3 | 3 | 3 | 3 | |||||||||||||||||||
| ⊆ ¬ | 2 | 2 | 1 | 1 | 2 | ||||||||||||||||||
| ⊆ ¬ ∥ | 19 | 15 | 1 | 5 | 1 | 4 | 1 | 3 | 4 | 1 | 20 | ||||||||||||
| ⊆ ¬ ∥ ∩ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ ¬ ∥ ∩ → ∧ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ ∥ | 4 | 1 | 1 | 2 | 62 | 55 | 8 | 12 | 4 | 13 | 5 | 10 | 1 | 2 | 2 | 5 | 66 | ||||||
| ⊆ ∥ ⊈ | 1 | 1 | 1 | 1 | 2 | ||||||||||||||||||
| ⊆ ∥ ≠ | 4 | 4 | 1 | 1 | 2 | 1 | 5 | ||||||||||||||||
| ⊆ ∥ ∩ | 1 | 1 | 1 | 1 | 1 | 2 | |||||||||||||||||
| ⊆ ∥ ∩ ∪ | 3 | 3 | 3 | ||||||||||||||||||||
| ⊆ ∥ ∪ | 7 | 5 | 2 | 3 | 1 | 1 | 1 | 7 | |||||||||||||||
| ⊆ ∥ ∪ → | 2 | 2 | 2 | 2 | |||||||||||||||||||
| ⊆ ∥ ∪ sp | 2 | 1 | 1 | 1 | 2 | ||||||||||||||||||
| ⊆ ∥ → | 1 | 1 | 4 | 2 | 2 | 1 | 1 | 1 | 5 | ||||||||||||||
| ⊆ ∥ → ~ ∧ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ ∥ sp | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ ⊈ | 5 | 5 | 2 | 2 | 1 | 5 | |||||||||||||||||
| ⊆ ⊈ ≠ | 3 | 3 | 2 | 1 | 3 | ||||||||||||||||||
| ⊆ ⊈ → | 1 | 1 | 1 | ||||||||||||||||||||
| ⊆ ⊈ → ~ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ ⊈ ⊥ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ ∩ | 6 | 6 | 1 | 1 | 1 | 2 | 1 | 6 | |||||||||||||||
| ⊆ ∩ ∪ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ ∩ → | 2 | 2 | 2 | 2 | |||||||||||||||||||
| ⊆ ∩ sp | 2 | 2 | 2 | 2 | |||||||||||||||||||
| ⊆ → | 8 | 7 | 2 | 1 | 3 | 1 | 1 | 8 | |||||||||||||||
| ⊆ → sp | 2 | 2 | 2 | 2 | |||||||||||||||||||
| ⊆ ∧ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ⊆ sp | 11 | 11 | 4 | 2 | 3 | 1 | 1 | 1 | 12 | ||||||||||||||
| = | 1 | 1 | 13 | 11 | 6 | 1 | 4 | 2 | 2 | 3 | 17 | ||||||||||||
| = ¬ | 3 | 3 | 2 | 1 | 3 | ||||||||||||||||||
| = ¬ ⊈ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| = ∥ | 4 | 4 | 2 | 1 | 1 | 2 | 6 | ||||||||||||||||
| = ≠ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| = ≠ ⊻ | 1 | 1 | 1 | ||||||||||||||||||||
| = ∩ ∪ → | 1 | 1 | 1 | 1 | |||||||||||||||||||
| = → | 1 | 1 | 1 | 1 | |||||||||||||||||||
| = → ∧ sp | 1 | 1 | 1 | ||||||||||||||||||||
| = sp | 2 | 2 | |||||||||||||||||||||
| ∦ ¬ ∥ ∪ → ⊻ | 1 | 1 | 1 | ||||||||||||||||||||
| ∦ ∥ ⊈ | 2 | 2 | 1 | 1 | 2 | ||||||||||||||||||
| ∦ ∥ ⊈ → | 1 | 1 | 1 | ||||||||||||||||||||
| ∦ ∥ ≠ | 2 | 2 | 1 | 1 | 2 | ||||||||||||||||||
| ∦ ∥ ∩ ∪ → | 1 | 1 | 1 | ||||||||||||||||||||
| ∦ ∥ ∪ → | 1 | 1 | 1 | ||||||||||||||||||||
| ∦ ∥ ∪ → ~ ∧ | 1 | 1 | 1 | ||||||||||||||||||||
| ¬ ∥ | 8 | 5 | 1 | 4 | 3 | 8 | |||||||||||||||||
| ¬ ∥ ∩ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ∥ | 1 | 1 | |||||||||||||||||||||
| ⊈ → ~ | 2 | 2 | 2 | ||||||||||||||||||||
| ≠ → ~ | 1 | 1 | 1 | ||||||||||||||||||||
| → | 2 | 1 | 1 | 21 | 10 | 3 | 1 | 1 | 3 | 2 | 3 | 6 | 2 | 2 | 1 | 24 | |||||||
| → ~ | 11 | 2 | 4 | 3 | 2 | 31 | 11 | 1 | 1 | 1 | 3 | 3 | 2 | 7 | 7 | 6 | 4 | 2 | 42 | ||||
| → ~ ∧ | 3 | 1 | 1 | 1 | 1 | 3 | |||||||||||||||||
| → ~ ∧ ∨ | 1 | 1 | 1 | ||||||||||||||||||||
| → ~ ∨ | 1 | 1 | 7 | 7 | 7 | 8 | |||||||||||||||||
| → ~ ∨ ⊻ ↔ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| → ~ ⊻ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| → ∧ | 1 | 1 | 4 | 2 | 1 | 1 | 1 | 1 | 1 | 4 | 9 | ||||||||||||
| → ∨ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ~ | 10 | 10 | 1 | 4 | 1 | 3 | 1 | 1 | 11 | ||||||||||||||
| ~ ∧ ∨ ⊻ ↔ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| ~ ∨ | 1 | 1 | 1 | 1 | 1 | 2 | |||||||||||||||||
| ~ ⊻ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| wszystko | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Tabela 23. Te same dane, procenty
| funktory | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| ⊆ | 7 | 25 | 13 | 20 | 25 | 41 | 17 | 20 | 32 | 21 | 17 | 50 | 43 | 3 | 25 | 17,9 | |||||||
| ⊆ = | 5 | 5 | 10 | 8 | 6 | 3 | 14 | 13 | 33 | 5 | 4,7 | ||||||||||||
| ⊆ = ¬ | 0 | 1 | 3 | 2 | 0,4 | ||||||||||||||||||
| ⊆ = ∥ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ = ∥ sp | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ = ∩ | 0 | 1 | 2 | 2 | 0,4 | ||||||||||||||||||
| ⊆ = ∪ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ = → | 2 | 0 | 2 | 21 | 53 | 1,9 | |||||||||||||||||
| ⊆ = sp | 1 | 2 | 3 | 2 | 7 | 5 | 1,3 | ||||||||||||||||
| ⊆ ∦ | 1 | 1 | 2 | 2 | 5 | 0,9 | |||||||||||||||||
| ⊆ ∦ ¬ ⊈ sp | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ ∦ ∥ ⊈ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ ∦ ∥ ∪ → ~ | 0 | 2 | 0,2 | ||||||||||||||||||||
| ⊆ ∦ ∥ → | 0 | 2 | 0,2 | ||||||||||||||||||||
| ⊆ ∦ ∥ → ~ | 0 | 2 | 0,2 | ||||||||||||||||||||
| ⊆ ∦ → | 0 | 0 | 3 | 2 | 0,4 | ||||||||||||||||||
| ⊆ ∦ sp | 1 | 1 | 7 | 0,6 | |||||||||||||||||||
| ⊆ ¬ | 0 | 1 | 2 | 2 | 0,4 | ||||||||||||||||||
| ⊆ ¬ ∥ | 5 | 5 | 3 | 8 | 2 | 6 | 2 | 6 | 9 | 5 | 4,3 | ||||||||||||
| ⊆ ¬ ∥ ∩ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ ¬ ∥ ∩ → ∧ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ ∥ | 14 | 25 | 10 | 25 | 15 | 17 | 21 | 20 | 8 | 21 | 12 | 19 | 50 | 14 | 15 | 11 | 14,1 | ||||||
| ⊆ ∥ ⊈ | 0 | 0 | 2 | 5 | 0,4 | ||||||||||||||||||
| ⊆ ∥ ≠ | 1 | 1 | 2 | 2 | 4 | 5 | 1,1 | ||||||||||||||||
| ⊆ ∥ ∩ | 4 | 13 | 0 | 0 | 2 | 0,4 | |||||||||||||||||
| ⊆ ∥ ∩ ∪ | 1 | 6 | 0,6 | ||||||||||||||||||||
| ⊆ ∥ ∪ | 2 | 2 | 3 | 6 | 2 | 3 | 25 | 1,5 | |||||||||||||||
| ⊆ ∥ ∪ → | 0 | 5 | 11 | 0,4 | |||||||||||||||||||
| ⊆ ∥ ∪ sp | 0 | 0 | 2 | 2 | 0,4 | ||||||||||||||||||
| ⊆ ∥ → | 4 | 13 | 1 | 1 | 3 | 2 | 3 | 5 | 1,1 | ||||||||||||||
| ⊆ ∥ → ~ ∧ | 0 | 3 | 5 | 0,2 | |||||||||||||||||||
| ⊆ ∥ sp | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ ⊈ | 1 | 2 | 4 | 3 | 2 | 1,1 | |||||||||||||||||
| ⊆ ⊈ ≠ | 1 | 1 | 4 | 2 | 0,6 | ||||||||||||||||||
| ⊆ ⊈ → | 4 | 17 | 0,2 | ||||||||||||||||||||
| ⊆ ⊈ → ~ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ ⊈ ⊥ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ ∩ | 1 | 2 | 3 | 2 | 2 | 5 | 7 | 1,3 | |||||||||||||||
| ⊆ ∩ ∪ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ ∩ → | 0 | 1 | 5 | 0,4 | |||||||||||||||||||
| ⊆ ∩ sp | 0 | 1 | 5 | 0,4 | |||||||||||||||||||
| ⊆ → | 2 | 2 | 4 | 2 | 7 | 2 | 2 | 1,7 | |||||||||||||||
| ⊆ → sp | 0 | 1 | 5 | 0,4 | |||||||||||||||||||
| ⊆ ∧ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ⊆ sp | 3 | 3 | 10 | 4 | 7 | 2 | 7 | 5 | 2,6 | ||||||||||||||
| = | 4 | 10 | 3 | 3 | 10 | 2 | 8 | 5 | 13 | 15 | 3,6 | ||||||||||||
| = ¬ | 1 | 1 | 3 | 2 | 0,6 | ||||||||||||||||||
| = ¬ ⊈ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| = ∥ | 1 | 1 | 3 | 2 | 2 | 10 | 1,3 | ||||||||||||||||
| = ≠ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| = ≠ ⊻ | 4 | 10 | 0,2 | ||||||||||||||||||||
| = ∩ ∪ → | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| = → | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| = → ∧ sp | 4 | 17 | 0,2 | ||||||||||||||||||||
| = sp | 10 | 0,4 | |||||||||||||||||||||
| ∦ ¬ ∥ ∪ → ⊻ | 0 | 2 | 0,2 | ||||||||||||||||||||
| ∦ ∥ ⊈ | 0 | 1 | 2 | 2 | 0,4 | ||||||||||||||||||
| ∦ ∥ ⊈ → | 0 | 2 | 0,2 | ||||||||||||||||||||
| ∦ ∥ ≠ | 0 | 1 | 2 | 2 | 0,4 | ||||||||||||||||||
| ∦ ∥ ∩ ∪ → | 0 | 2 | 0,2 | ||||||||||||||||||||
| ∦ ∥ ∪ → | 0 | 2 | 0,2 | ||||||||||||||||||||
| ∦ ∥ ∪ → ~ ∧ | 0 | 2 | 0,2 | ||||||||||||||||||||
| ¬ ∥ | 2 | 2 | 2 | 8 | 6 | 1,7 | |||||||||||||||||
| ¬ ∥ ∩ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ∥ | 5 | 0,2 | |||||||||||||||||||||
| ⊈ → ~ | 0 | 4 | 0,4 | ||||||||||||||||||||
| ≠ → ~ | 0 | 2 | 0,2 | ||||||||||||||||||||
| → | 7 | 10 | 17 | 5 | 3 | 5 | 2 | 2 | 6 | 14 | 23 | 13 | 5 | 11 | 5 | 5,1 | |||||||
| → ~ | 39 | 50 | 40 | 38 | 33 | 7 | 3 | 3 | 2 | 2 | 5 | 7 | 4 | 54 | 15 | 16 | 21 | 50 | 9,0 | ||||
| → ~ ∧ | 1 | 0 | 2 | 8 | 2 | 0,6 | |||||||||||||||||
| → ~ ∧ ∨ | 0 | 2 | 0,2 | ||||||||||||||||||||
| → ~ ∨ | 4 | 10 | 2 | 18 | 37 | 1,7 | |||||||||||||||||
| → ~ ∨ ⊻ ↔ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| → ~ ⊻ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| → ∧ | 4 | 17 | 1 | 1 | 2 | 2 | 2 | 3 | 5 | 20 | 1,9 | ||||||||||||
| → ∨ | 0 | 3 | 5 | 0,2 | |||||||||||||||||||
| ~ | 2 | 3 | 3 | 7 | 2 | 5 | 2 | 5 | 2,4 | ||||||||||||||
| ~ ∧ ∨ ⊻ ↔ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| ~ ∨ | 10 | 0 | 0 | 2 | 0,4 | ||||||||||||||||||
| ~ ⊻ | 0 | 0 | 2 | 0,2 | |||||||||||||||||||
| 100%= | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Z tabeli tej nie da się wiele wyczytać. Komentarzem do niej są tabele następne, ukazujące różne aspekty rozkładu funktorów w regułach.
7. Częstość występowania funktorów w regułach
Tabela 24. Wg miejsc
| funktor | miejsca | ilość miejsc |
| ⊆ | 5, 8, 9, 14, 14, 14, 15, 16, 17, 18, 18, 18, 18, 18, 18, 18, 19, 20, 21, 22, 22, 22, 23, 25, 25, 25, 25, 26, 26, 26, 26, 26, 27, 27, 27, 27, 27, 27, 28, 29, 31, 31, 31, 31, 32, 32, 33, 33, 34, 35, 36, 37, 37, 38, 38, 38, 39, 40, 40, 41, 42, 42, 45, 45, 46, 46, 46, 46, 47, 48, 48, 48, 48, 50, 50, 51, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 54, 56, 57, 58, 59, 60, 61, 62, 64, 64, 65, 66, 66, 67, 67, 68, 68, 69, 69, 71, 72, 73, 74, 74, 74, 76, 76, 76, 77, 79, 79, 79, 80, 81, 82, 83, 84, 85, 86, 86, 87, 88, 89, 91, 91, 92, 93, 93, 94, 95, 95, 96, 96, 97, 98, 98, 99, 99, 99, 99, 100, 101, 101, 102, 102, 103, 103, 104, 105, 107, 107, 107, 110, 111, 112, 112, 113, 114, 114, 116, 116, 117, 118, 118, 118, 119, 119, 119, 119, 119, 120, 120, 120, 120, 120, 120, 121, 121, 121, 121, 121, 123, 123, 123, 124, 124, 125, 125, 125, 125, 125, 126, 126, 126, 126, 127, 128, 128, 129, 129, 129, 129, 130, 131, 131, 132, 133, 133, 133, 135, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 138, 138, 138, 138, 138, 138, 139, 140, 140, 140, 140, 140, 140, 140, 141, 141, 141, 141, 141, 142, 143, 144, 144, 145, 146, 146, 147, 148, 148, 148, 149, 150, 151, 152, 153, 154, 155, 156, 156, 156, 156, 157, 158, 159, 207, 207, 208, 209, 216, 216, 216, 216, 217, 217, 217, 218, 218, 218, 219, 219, 219, 220, 220, 220, 220, 302, 303, 304, 305, 305, 306 | 307 |
| = | 3, 3, 10, 18, 18, 19, 25, 25, 25, 40, 43, 43, 43, 46, 51, 51, 51, 51, 51, 79, 108, 108, 108, 114, 114, 118, 119, 120, 120, 120, 121, 121, 125, 127, 127, 129, 129, 129, 129, 133, 133, 133, 133, 133, 134, 134, 134, 137, 137, 137, 138, 146, 148, 149, 217, 217, 217, 217, 217, 218, 218, 218, 219, 219, 219, 220, 220, 220, 220, 301, 301, 301, 301, 301, 301, 301, 304, 305 | 78 |
| ∦ | 32, 53, 53, 53, 53, 53, 53, 53, 53, 53, 70, 74, 86, 87, 88, 115, 128, 137, 137, 137, 137, 137, 156 | 23 |
| ¬ | 25, 25, 40, 43, 43, 46, 46, 46, 48, 48, 50, 51, 53, 53, 53, 53, 53, 53, 53, 53, 59, 67, 79, 86, 93, 93, 94, 98, 108, 108, 113, 114, 121, 124, 124, 126, 128, 133, 141, 157, 303 | 41 |
| ∥ | 8, 14, 14, 14, 16, 17, 18, 18, 25, 26, 26, 26, 26, 26, 29, 33, 33, 37, 37, 38, 38, 39, 40, 40, 45, 45, 46, 46, 46, 46, 46, 48, 48, 48, 50, 50, 50, 51, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 59, 64, 65, 67, 67, 70, 76, 76, 76, 88, 88, 91, 91, 92, 93, 93, 93, 94, 96, 96, 98, 99, 99, 100, 103, 103, 111, 112, 113, 115, 116, 117, 118, 119, 120, 121, 124, 124, 124, 125, 125, 125, 125, 126, 126, 126, 127, 128, 128, 129, 129, 129, 131, 131, 133, 137, 137, 140, 141, 141, 142, 144, 144, 145, 146, 150, 152, 156, 156, 156, 156, 157, 207, 207, 209, 216, 216, 216, 216, 301, 301, 302, 303, 303, 306 | 149 |
| ⊈ | 9, 35, 43, 47, 53, 53, 53, 70, 81, 82, 83, 85, 86, 86, 88, 88, 89, 101, 128, 143, 306 | 21 |
| ≠ | 3, 46, 51, 53, 83, 85, 111, 115, 117, 142, 143, 156, 302 | 13 |
| ∩ | 14, 28, 53, 53, 53, 53, 59, 107, 112, 118, 118, 121, 124, 124, 134, 138, 138, 138, 138, 138, 138, 140, 154 | 23 |
| ∪ | 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 76, 118, 118, 119, 120, 120, 125, 134, 156, 209, 216, 216 | 22 |
| → | 1, 1, 1, 1, 2, 2, 4, 6, 9, 9, 10, 10, 11, 12, 14, 16, 16, 16, 32, 32, 38, 38, 38, 38, 38, 38, 44, 45, 49, 51, 51, 51, 51, 51, 52, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 55, 56, 58, 59, 63, 66, 66, 75, 78, 81, 90, 108, 108, 119, 121, 122, 130, 130, 134, 136, 136, 138, 138, 140, 140, 146, 149, 153, 201, 202, 203, 204, 205, 206, 207, 207, 207, 207, 207, 210, 211, 212, 213, 213, 213, 213, 213, 213, 213, 213, 214, 214, 214, 215, 215, 215, 216, 216, 216, 216, 218, 218, 219, 219, 220, 220, 220, 220, 307, 307, 307, 307, 307 | 138 |
| ~ | 1, 1, 1, 1, 1, 2, 4, 6, 9, 12, 14, 16, 16, 24, 32, 35, 37, 38, 38, 38, 43, 44, 44, 45, 49, 51, 52, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 55, 63, 81, 88, 90, 99, 101, 108, 129, 130, 130, 131, 136, 136, 201, 203, 204, 205, 206, 207, 207, 207, 210, 211, 213, 213, 213, 213, 213, 213, 213, 213, 214, 214, 215, 216, 307 | 79 |
| ∧ | 10, 10, 44, 51, 53, 53, 53, 53, 59, 78, 108, 130, 203, 215, 216, 307, 307, 307, 307 | 19 |
| ∨ | 1, 2, 44, 44, 53, 108, 212, 213, 213, 213, 213, 213, 214, 214 | 14 |
| ⊻ | 3, 35, 44, 44, 53, 136 | 6 |
| ↔ | 44, 44 | 2 |
| ⊥ | 89 | 1 |
| specyficzny | 10, 19, 31, 31, 31, 31, 40, 53, 66, 68, 86, 119, 119, 119, 119, 126, 137, 137, 137, 137, 137, 137, 138, 138, 139, 140, 140, 141, 151, 301, 301, 305, 305 | 33 |
| Dowolny | 468 | |
Tabela 25. Wg grup tekstów
| funktory | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| ⊆ | 9 | 2 | 1 | 5 | 1 | 292 | 251 | 37 | 38 | 41 | 51 | 39 | 31 | 2 | 12 | 2 | 20 | 19 | 4 | 13 | 2 | 6 | 307 |
| = | 3 | 2 | 1 | 66 | 51 | 6 | 14 | 8 | 7 | 4 | 10 | 2 | 15 | 15 | 9 | 78 | |||||||
| ∦ | 23 | 14 | 1 | 4 | 4 | 5 | 9 | 23 | |||||||||||||||
| ¬ | 40 | 32 | 2 | 6 | 4 | 8 | 2 | 10 | 8 | 1 | 41 | ||||||||||||
| ∥ | 6 | 1 | 1 | 4 | 137 | 104 | 9 | 26 | 16 | 22 | 7 | 21 | 1 | 2 | 2 | 26 | 5 | 4 | 1 | 6 | 149 | ||
| ⊈ | 1 | 1 | 19 | 16 | 2 | 8 | 3 | 3 | 3 | 1 | 21 | ||||||||||||
| ≠ | 1 | 1 | 11 | 10 | 1 | 4 | 1 | 4 | 1 | 1 | 13 | ||||||||||||
| ∩ | 1 | 1 | 22 | 18 | 1 | 1 | 5 | 2 | 8 | 1 | 4 | 23 | |||||||||||
| ∪ | 22 | 9 | 3 | 6 | 10 | 3 | 2 | 1 | 22 | ||||||||||||||
| → | 18 | 2 | 6 | 4 | 6 | 115 | 45 | 2 | 7 | 4 | 9 | 12 | 9 | 2 | 11 | 30 | 29 | 19 | 8 | 2 | 5 | 138 | |
| ~ | 13 | 2 | 6 | 3 | 2 | 65 | 28 | 2 | 6 | 2 | 9 | 3 | 6 | 8 | 15 | 14 | 12 | 2 | 1 | 79 | |||
| ∧ | 2 | 2 | 13 | 6 | 2 | 1 | 1 | 2 | 1 | 4 | 2 | 2 | 4 | 19 | |||||||||
| ∨ | 2 | 2 | 12 | 3 | 1 | 2 | 1 | 8 | 8 | 14 | |||||||||||||
| ⊻ | 1 | 1 | 5 | 4 | 1 | 1 | 2 | 1 | 6 | ||||||||||||||
| ↔ | 2 | 2 | 2 | 2 | |||||||||||||||||||
| ⊥ | 1 | 1 | 1 | 1 | |||||||||||||||||||
| specyf. | 1 | 1 | 28 | 27 | 5 | 1 | 5 | 1 | 13 | 1 | 1 | 1 | 4 | 33 | |||||||||
| wszystko | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Tabela 26. Te same dane, procenty
| funktory | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| ⊆ | 32 | 50 | 10 | 63 | 17 | 69,5 | 78,0 | 95 | 63 | 84 | 81 | 91 | 60 | 100 | 86 | 15 | 43 | 50 | 21 | 87 | 50 | 30 | 65,6 |
| = | 11 | 20 | 17 | 15,7 | 15,8 | 15 | 23 | 16 | 11 | 9 | 19 | 14 | 39 | 100 | 45 | 16,7 | |||||||
| ∦ | 5,5 | 4,3 | 3 | 7 | 8 | 12 | 19 | 4,9 | |||||||||||||||
| ¬ | 9,5 | 9,9 | 5 | 10 | 8 | 13 | 5 | 19 | 17 | 5 | 8,8 | ||||||||||||
| ∥ | 21 | 25 | 10 | 50 | 32,6 | 32,3 | 23 | 43 | 33 | 35 | 16 | 40 | 50 | 14 | 15 | 55 | 13 | 21 | 25 | 30 | 31,8 | ||
| ⊈ | 4 | 17 | 4,5 | 5,0 | 3 | 16 | 5 | 6 | 6 | 5 | 4,5 | ||||||||||||
| ≠ | 4 | 10 | 2,6 | 3,1 | 2 | 8 | 2 | 8 | 2 | 5 | 2,8 | ||||||||||||
| ∩ | 4 | 13 | 5,2 | 5,6 | 3 | 2 | 10 | 3 | 19 | 7 | 9 | 4,9 | |||||||||||
| ∪ | 5,2 | 2,8 | 5 | 12 | 21 | 8 | 11 | 25 | 4,7 | ||||||||||||||
| → | 64 | 50 | 60 | 50 | 100 | 27,4 | 14,0 | 5 | 12 | 8 | 14 | 28 | 17 | 14 | 85 | 64 | 76 | 100 | 53 | 50 | 25 | 29,5 | |
| ~ | 46 | 60 | 38 | 33 | 15,5 | 8,7 | 5 | 10 | 4 | 14 | 7 | 12 | 62 | 32 | 37 | 63 | 50 | 5 | 16,9 | ||||
| ∧ | 7 | 33 | 3,1 | 1,9 | 3 | 2 | 2 | 4 | 8 | 9 | 5 | 11 | 20 | 4,1 | |||||||||
| ∨ | 7 | 20 | 2,9 | 0,9 | 2 | 4 | 2 | 21 | 42 | 3,0 | |||||||||||||
| ⊻ | 4 | 10 | 1,2 | 1,2 | 2 | 2 | 4 | 2 | 1,3 | ||||||||||||||
| ↔ | 0,5 | 0,6 | 4 | 0,4 | |||||||||||||||||||
| ⊥ | 0,2 | 0,3 | 2 | 0,2 | |||||||||||||||||||
| specyf. | 17 | 6,7 | 8,4 | 13 | 2 | 10 | 2 | 30 | 2 | 7 | 2 | 20 | 7,1 | ||||||||||
| 100%= | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Spośród dwuargumentowych funktorów zdaniotwórczych od argumentów nazwowych najpopularniejszy zdecydowanie jest funktor ⊆ (tradycyjne a): występuje w 65,6% reguł (78,0% u sokratyków). Po nim następują: ∥ (tradycyjne e): 31,8% (32,3%), = (nie występuje w sylogistyce tradycyjnej): 16,7% (15,8%), ∦ (tradycyjne i): 4,9% (4,3%), ⊈ (tradycyjne o): 4,5% (5,0%) oraz ≠ (nie występuje w sylogistyce tradycyjnej): 2,8% (3,1%).
Wykorzystując informacje o współwystępowaniu funktorów z tabeli 27. możemy stwierdzić, że jakiś tradycyjny funktor ogólny (⊆ lub ∥) występuje w sumie w 412 z 468 reguł (88%), zaś szczegółowy (⊈ lub ∦) w 39 (8%). Z kolei funktory twierdzące (⊆ lub ∦) występują w 316 regułach (68%), a przeczące (∥ lub ⊈) w 164 (35%). Nietradycyjne ≠/≠: 89 (19%).
Z innych funktorów nazwowych należy wymienić negację nazwową (dopełnienie), występującą w 8,8% reguł (u sokratyków w 9,9%) oraz koniunkcję (iloczyn mnogościowy): 4,9% (5,6%) i alternatywę (sumę mnogościową): 4,7% (2,8%). Którakolwiek z dwóch ostatnich występuje w 8,3% wszystkich reguł.
Spośród funktorów od argumentów zdaniowych najpopularniejsza jest implikacja (29,5% i 14,0%) i negacja (16,9% i 8,7%). Pozostałe znajdują się łącznie w 8,8% (4,6%) reguł. Przy rozważaniu koniunkcji i alternatywy pamiętać jednak należy (podobnie zresztą w przypadku koniunkcji i alternatywy nazwowej), że pominięte zostały użycia reguł dołączania alternatywy (np. α ⊢ α∨β) i opuszczania koniunkcji (np. α∧β ⊢ α), jako że niezwykle trudno rozróżnić tekst, który ma być sformalizowany np. na sposób „α∧β ⊢ α” od tego, którego właściwą formalizacją jest „α, β ⊢ α” (w niektórych formalizacjach dedukcji naturalnej przyjmuje się zresztą na mocy konwencji, że te dwa zapisy są równoważne).
W 7,1% (8,4%) reguł znajduje się też funktor specyficzny, który prawie zawsze jest funktorem nazwotwórczym od argumentu nazwowego (raz tylko, u Herodota, są to dwie stałe matematyczne: „90 dni” i „3 miesiące”).
8. Współwystępowanie funktorów
Tabela 27. Ilość reguł, w których współwystępują dane dwa funktory
Na przecięciach wierszy i kolumn dotyczących tego samego funktora znajdują się wartości dla reguł o jednym tylko funktorze.
| funktor | funktor | wszystko | ||||||||||||||||
| ⊆ | = | ∦ | ¬ | ∥ | ⊈ | ≠ | ∩ | ∪ | → | ~ | ∧ | ∨ | ⊻ | ↔ | ⊥ | sp. | ||
| ⊆ | 84 | 44 | 14 | 27 | 124 | 15 | 8 | 20 | 17 | 37 | 4 | 3 | 1 | 30 | 307 | |||
| = | 44 | 17 | 6 | 8 | 1 | 2 | 3 | 2 | 12 | 1 | 1 | 10 | 78 | |||||
| ∦ | 14 | 2 | 13 | 5 | 2 | 1 | 5 | 10 | 3 | 1 | 1 | 4 | 23 | |||||
| ¬ | 27 | 6 | 2 | 32 | 2 | 3 | 1 | 2 | 1 | 1 | 1 | 41 | ||||||
| ∥ | 124 | 8 | 13 | 32 | 1 | 6 | 7 | 9 | 19 | 17 | 4 | 3 | 1 | 4 | 149 | |||
| ⊈ | 15 | 1 | 5 | 2 | 6 | 3 | 5 | 3 | 1 | 1 | 21 | |||||||
| ≠ | 8 | 2 | 2 | 7 | 3 | 1 | 1 | 1 | 13 | |||||||||
| ∩ | 20 | 3 | 1 | 3 | 9 | 6 | 5 | 1 | 2 | 23 | ||||||||
| ∪ | 17 | 2 | 5 | 1 | 19 | 6 | 8 | 2 | 1 | 1 | 2 | 22 | ||||||
| → | 37 | 12 | 10 | 2 | 17 | 5 | 1 | 5 | 8 | 24 | 64 | 17 | 11 | 3 | 1 | 3 | 138 | |
| ~ | 4 | 3 | 4 | 3 | 1 | 2 | 64 | 11 | 7 | 13 | 4 | 2 | 79 | |||||
| ∧ | 3 | 1 | 1 | 1 | 3 | 1 | 1 | 17 | 7 | 2 | 1 | 1 | 1 | 19 | ||||
| ∨ | 11 | 13 | 2 | 2 | 2 | 14 | ||||||||||||
| ⊻ | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 4 | 1 | 2 | 2 | 6 | ||||||
| ↔ | 1 | 2 | 1 | 2 | 2 | 2 | ||||||||||||
| ⊥ | 1 | 1 | 1 | |||||||||||||||
| specyf. | 30 | 10 | 4 | 1 | 4 | 1 | 2 | 2 | 3 | 1 | 33 | |||||||
| wszystko | 307 | 78 | 23 | 41 | 149 | 21 | 13 | 23 | 22 | 138 | 79 | 19 | 14 | 6 | 2 | 1 | 33 | 468 |
Tabela 28. Prawdopodobieństwo (w %) wystąpienia funktora z lewej strony tabeli przy założeniu, że w danej figurze jest funktor z nagłówka tabeli
| funktor | funktor | wszystko | ||||||||||||||||
| ⊆ | = | ∦ | ¬ | ∥ | ⊈ | ≠ | ∩ | ∪ | → | ~ | ∧ | ∨ | ⊻ | ↔ | ⊥ | sp. | ||
| ⊆ | 27 | 56 | 61 | 66 | 83 | 71 | 62 | 87 | 77 | 27 | 5 | 16 | 100 | 91 | 66 | |||
| = | 14 | 22 | 15 | 5 | 5 | 15 | 13 | 9 | 9 | 5 | 17 | 30 | 17 | |||||
| ∦ | 5 | 5 | 9 | 24 | 15 | 4 | 23 | 7 | 4 | 5 | 17 | 12 | 5 | |||||
| ¬ | 9 | 8 | 9 | 21 | 10 | 13 | 5 | 1 | 5 | 17 | 3 | 9 | ||||||
| ∥ | 40 | 10 | 57 | 78 | 1 | 29 | 54 | 39 | 86 | 12 | 5 | 16 | 17 | 12 | 32 | |||
| ⊈ | 5 | 1 | 22 | 5 | 4 | 23 | 4 | 4 | 100 | 3 | 4 | |||||||
| ≠ | 3 | 3 | 9 | 5 | 14 | 1 | 1 | 17 | 3 | |||||||||
| ∩ | 7 | 4 | 4 | 7 | 6 | 27 | 4 | 5 | 6 | 5 | ||||||||
| ∪ | 6 | 3 | 22 | 2 | 13 | 26 | 6 | 3 | 5 | 17 | 6 | 5 | ||||||
| → | 12 | 15 | 43 | 5 | 11 | 24 | 8 | 22 | 36 | 17 | 81 | 89 | 79 | 50 | 50 | 9 | 29 | |
| ~ | 1 | 13 | 3 | 14 | 8 | 9 | 46 | 14 | 37 | 93 | 67 | 100 | 17 | |||||
| ∧ | 1 | 1 | 4 | 2 | 2 | 4 | 5 | 12 | 9 | 14 | 17 | 50 | 3 | 4 | ||||
| ∨ | 8 | 16 | 11 | 33 | 100 | 3 | ||||||||||||
| ⊻ | 1 | 4 | 2 | 1 | 8 | 5 | 2 | 5 | 5 | 14 | 100 | 1 | ||||||
| ↔ | 1 | 3 | 5 | 14 | 33 | 0 | ||||||||||||
| ⊥ | 0 | 5 | 0 | |||||||||||||||
| specyf. | 10 | 13 | 17 | 2 | 3 | 5 | 9 | 9 | 2 | 5 | 7 | |||||||
| 100%= | 307 | 78 | 23 | 41 | 149 | 21 | 13 | 23 | 22 | 138 | 79 | 19 | 14 | 6 | 2 | 1 | 33 | 468 |
9. Ilość różnych funktorów w regułach
Tabela 29. Wg miejsc
| ilość funktorów | miejsca | ilość miejsc |
| 1 | 2, 3, 5, 11, 15, 18, 18, 18, 20, 21, 22, 22, 22, 23, 24, 27, 27, 27, 27, 27, 27, 32, 34, 36, 37, 41, 42, 42, 43, 43, 46, 51, 51, 51, 51, 51, 51, 53, 53, 53, 53, 53, 53, 54, 57, 60, 61, 62, 64, 66, 68, 69, 69, 71, 72, 73, 74, 74, 75, 77, 79, 80, 84, 88, 95, 95, 97, 98, 99, 99, 99, 101, 101, 102, 102, 104, 105, 107, 107, 110, 112, 116, 120, 120, 121, 121, 122, 123, 123, 123, 125, 125, 126, 129, 129, 130, 130, 130, 130, 131, 132, 133, 133, 133, 134, 134, 135, 140, 140, 140, 141, 141, 146, 147, 148, 148, 149, 153, 153, 155, 156, 158, 159, 202, 207, 207, 208, 214, 215, 217, 217, 301, 301, 301, 303, 307, 307 | 137 |
| 2 | 1, 1, 1, 1, 1, 4, 6, 8, 9, 10, 12, 14, 14, 14, 16, 16, 17, 18, 18, 18, 18, 25, 25, 26, 26, 26, 26, 26, 28, 29, 31, 31, 31, 31, 32, 33, 33, 35, 35, 37, 37, 38, 38, 38, 38, 39, 43, 45, 45, 45, 46, 46, 47, 48, 48, 48, 49, 50, 50, 50, 51, 51, 52, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 55, 56, 58, 63, 64, 65, 66, 66, 67, 68, 74, 76, 76, 78, 79, 79, 82, 86, 87, 90, 91, 91, 92, 93, 93, 96, 96, 99, 99, 100, 101, 103, 103, 107, 108, 108, 108, 108, 108, 114, 116, 119, 119, 119, 120, 120, 121, 121, 121, 124, 125, 125, 125, 126, 127, 127, 129, 129, 129, 129, 129, 130, 131, 131, 133, 133, 136, 137, 137, 137, 137, 138, 139, 140, 140, 141, 141, 144, 144, 145, 146, 146, 148, 149, 150, 151, 152, 154, 156, 156, 201, 204, 205, 206, 207, 207, 207, 207, 207, 210, 211, 212, 213, 213, 213, 215, 215, 217, 217, 217, 218, 219, 301, 301, 301, 301, 304, 305, 307, 307, 307, 307 | 202 |
| 3 | 2, 3, 9, 14, 16, 19, 25, 25, 32, 38, 38, 40, 43, 46, 46, 46, 48, 51, 51, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 53, 67, 70, 76, 83, 85, 88, 88, 89, 93, 94, 98, 111, 112, 113, 114, 115, 117, 118, 118, 118, 119, 120, 120, 121, 124, 125, 126, 126, 128, 133, 136, 137, 137, 137, 137, 137, 137, 138, 138, 138, 138, 138, 140, 140, 141, 142, 143, 156, 156, 157, 203, 209, 213, 213, 213, 213, 213, 214, 214, 216, 218, 218, 219, 219, 220, 220, 220, 220, 302, 303, 305, 306 | 102 |
| 4 | 10, 40, 53, 53, 53, 53, 53, 53, 53, 53, 81, 119, 124, 128, 134, 216, 216 | 17 |
| 5 | 44, 44, 53, 53, 86, 216 | 6 |
| 6 | 53, 53, 53, 59 | 4 |
| 1–6 | Wszystkie | 468 |
Tabela 30. Wg grup tekstów
| ilość funktorów | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| 1 | 5 | 1 | 2 | 1 | 1 | 126 | 112 | 17 | 23 | 13 | 23 | 10 | 17 | 1 | 8 | 3 | 6 | 5 | 2 | 2 | 1 | 6 | 137 |
| 2 | 17 | 3 | 6 | 5 | 3 | 175 | 136 | 18 | 24 | 17 | 29 | 18 | 23 | 1 | 6 | 9 | 17 | 13 | 6 | 5 | 2 | 10 | 202 |
| 3 | 5 | 2 | 2 | 1 | 93 | 64 | 4 | 11 | 16 | 9 | 14 | 10 | 1 | 11 | 17 | 8 | 8 | 1 | 4 | 102 | |||
| 4 | 1 | 1 | 16 | 6 | 2 | 2 | 2 | 8 | 2 | 2 | 17 | ||||||||||||
| 5 | 6 | 3 | 1 | 2 | 2 | 1 | 1 | 6 | |||||||||||||||
| 6 | 4 | 1 | 1 | 3 | 4 | ||||||||||||||||||
| wszystko | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Tabela 31. Te same dane, procenty
| ilość funktorów | grupy | wszystko | |||||||||||||||||||||
| 1–4 | 1 | 2 | 3 | 4 | 5–17 | 5–12 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15–17 | 15 | 16 | 17 | 18 | ||
| 1 | 18 | 25 | 20 | 13 | 17 | 30 | 35 | 44 | 38 | 27 | 37 | 23 | 33 | 50 | 57 | 23 | 13 | 13 | 11 | 13 | 25 | 30 | 29 |
| 2 | 61 | 75 | 60 | 63 | 50 | 42 | 42 | 46 | 40 | 35 | 46 | 42 | 44 | 50 | 43 | 69 | 36 | 34 | 32 | 33 | 50 | 50 | 43 |
| 3 | 18 | 20 | 25 | 17 | 22 | 20 | 10 | 18 | 33 | 14 | 33 | 19 | 8 | 23 | 45 | 42 | 53 | 25 | 20 | 22 | |||
| 4 | 17 | 4 | 2 | 3 | 4 | 3 | 17 | 5 | 11 | 4 | |||||||||||||
| 5 | 1 | 1 | 2 | 4 | 4 | 3 | 5 | 1 | |||||||||||||||
| 6 | 1 | 0 | 2 | 6 | 1 | ||||||||||||||||||
| 100%= | 28 | 4 | 10 | 8 | 6 | 420 | 322 | 39 | 60 | 49 | 63 | 43 | 52 | 2 | 14 | 13 | 47 | 38 | 19 | 15 | 4 | 20 | 468 |
Brać pod uwagę należy w zasadzie wyłącznie reguły o 1–3 różnych funktorach (tylko w 6% przypadków może być ich więcej).
