II. Zależności statystyczne

Marek Jerzy. Minakowski, Prehistoria logiki formalnej

VII. Rozstrzygnięcia

1. Czy przed Arystotelesem była logika?

1.1. Czy ktoś przed Arystotelesem stworzył system logiczny?

a) świadectwa

Jedynym świadectwem explicite na temat tego, kto stworzył pierwszy system logiczny, jest sławna wypowiedź Arystotelesa z końca Topik (O dowodach sofistycznych), cytowana tutaj, w której, wedle powszechnej interpretacji, przypisuje on to osiągnięcie sobie.

Arystoteles pisze, że nikt do jego czasów nie prowadził badań nad sztuką wyprowadzania koniecznych wniosków z oczywistych przesłanek, podczas gdy badań nad argumentacją retoryczną było wiele. Nie wiadomo dokładnie, czy słowa te w zamyśle Arystotelesa miały się odnosić do samych Topik, czy też do całego Organonu (jak się zwykle uważa). Niezależnie jednak od tej interpretacji, do Topik odnoszą się na pewno, a jeżeli tak, to można podsumować, że zdaniem Arystotelesa nikt przed nim nie tylko nie stworzył formalnego systemu (jak on w Analitykach), ale nie zebrał nawet przykładów naiwnego stosowania logiki (jak on w Topikach).

Owo jedyne świadectwo jest jednak zbyt wątłą podstawą do opierania na nim całej naszej wiedzy o początkach logiki, niezależnie czy się wierzy, że słowa te napisał Arystoteles, a jeśli tak, to czy wierzy się Arystotelesowi. Jest wiele powodów by powątpiewać w moc tego argumentu: słowa te mógł wszak dopisać któryś z redaktorów pism Arystotelesa (zwłaszcza perypatetyk zainteresowany chwaleniem założyciela, a przez to własnej szkoły), mógł też Arystoteles sam napisać je nieszczerze, a przynajmniej nieobiektywnie: był on wszak stroną zainteresowaną.

Brak innych wypowiedzi na ten temat logiki i jej historii, niezależnych od Arystotelesa, może być skutkiem ich zaginięcia: to co mamy, to przecież tylko strzępy. Zachowana część pism samego Arystotelesa też cudem dotarła do nas. Nauki takie mogły zresztą nie być nigdy spisane: Platon nie spisywał swoich wykładów, wszystko wykładał ustnie (miał zresztą do tego swoją ideologię). Sokrates w ogóle niczego nie pisał.

W braku pism z pierwszej ręki korzystamy ze starożytnych komentarzy. Ich opinię (podobnie jak autorów późniejszych) przedstawiłem w rozdz. II. Przy odwoływaniu się do nich należy jednak pamiętać, że w ogromnej części opierały się one na źródłach Akademii lub Liceum, miały więc jeszcze większe powody do stronniczości.

b) ślady użycia takiego systemu

Spróbujmy więc poszukać przynajmniej śladów użycia takiego systemu. W tym celu powinniśmy najpierw zdefiniować cel poszukiwań i kryterium, po jakim rozpoznamy, że do niego dotarliśmy.

Przyjmijmy hipotezę najprostszą do obrony, której obalenie najwięcej nam przyniesie: suponowany system byłby systemem aksjomatycznym w najliberalniejszym tego słowa znaczeniu — każda jego teza byłaby aksjomatem. Mielibyśmy wtedy do czynienia z luźnym zbiorem reguł logicznych, w których nie byłoby pierwotnych (niedowodliwych) i wtórnych (wyprowadzalnych), czy też (jak u Arystotelesa) bardziej i mniej doskonałych, ale wszystkie miałyby równy status.

Byłby to zbiór toposów, schematów dowodzenia, szablonów argumentacyjnych — a więc wzorów, na podstawie których, po odpowiednim przystosowaniu otrzymywało się dowody logiczne. Czym miałby być taki topos? Byłaby to procedura, podana ogólnie lub na przykładach, z której po podstawieniu za zmienne (w formule ogólnej), lub zastąpieniu stałych pozalogicznych (przykładowych argumentów, jak „łabędź”, „czarne” itp. w Analitykach) uzyskiwałoby się dowód logiczny, składający się ze skończonej (ewentualnie przeliczalnej) liczby przesłanek i wniosku. Ustalić też należy sposób istnienia takiej procedury: przyjęcie, że musiała być zapisana byłoby zbyt ograniczające; z drugiej strony warunkiem koniecznym jest, żeby była stosowana świadomie, gdyby bowiem przyjąć, że wystarczy by była pewnym nawykiem postępowania w odpowiednich sytuacjach to zbiór takich procedur byłby nieodróżnialny od ewentualnej logiki naturalnej.

Nazwijmy taki system systemem minimalnym: byłby to skończony zbiór reguł istniejących co najmniej w świadomości użytkownika, z których (po zastosowaniu stosownej procedury podstawiania lub zastępowania) otrzymuje się poprawny dowód. Stwierdzenie braku nawet takiego systemu będzie dla nas równoznaczne przyznaniu historycznego pierwszeństwa Arystotelesowej sylogistyce.

Jak możnaby stwierdzić istnienie sytemu minimalnego? Jedynym, co można zrobić, jest próba odnalezienia jakichś niewytłumaczalnych inaczej lokalnych regularności (czyli nieregularności w skali ogólnej: gdy pewna część zachowuje się wyraźnie inaczej niż reszta) w zachowanych dowodach przedarystotelesowych; istnienie systemu minimalnego byłoby udowodnione, jeżeli okazałoby się, że jakaś grupa zachowanych dowodów zawiera np. identyczne sformułowania, przebiega w jakiś charakterystyczny sposób lub zawiera nieproporcjonalnie wiele jakichś reguł, które możnaby wtedy uznać za znane autorowi reguły dowodzenia, przy braku innych, jemu nieznanych.

Nie dysponujemy jak dotąd badaniami, które pozwoliłyby porównać dane uzyskane dla przedarystotelesowych Greków z losową, reprezentatywną grupą innych ludzi. Wszystkie analizy trzeba więc prowadzić wewnątrz korpusu prearystotelików.

Nieregularności świadczące o wykorzystywaniu przez jakiegoś autora gotowego zbioru toposów zamiast spontanicznego tworzenia argumentów na potrzeby chwili mogą być dwojakiego rodzaju:

• w formie logicznej — świadczące bezpośrednio o znajomości jednych, a nieznajomości innych reguł
• w formie językowej — świadczące o wykorzystywaniu przez autora gotowych (może nawet spetryfikowanych) schematów.

Trzeci sposób, mianowicie szukanie charakterystycznych błędów lub nadspodziewanie wysokiej poprawności, pozostaje niedostępny z uwagi na przyjętą metodologię zakładającą życzliwą interpretację tekstu i na to, że badane są teksty naukowe lub arcydzieła literackie, które autor zdążył starannie przygotować i przedyskutować, a miał dość czasu i motywacji, aby usunąć wszelkie wyraźne błędy.

Najwyraźniejsza nieregularność w formie logicznej dowodu to oczywiście dysproporcja pomiędzy częstością znajdywania dowodów nazwowych i zdaniowych, a dokładniej nadzwyczajna ilość dowodów nazwowych w tekstach sokratyków. Poniżej rozważymy możliwość, że cała sylogistyka była takim właśnie systemem minimalnym, zostańmy jednak jeszcze na chwilę przy rachunku zdań.

Bardzo możliwe, że przed Arystotelesem znany był już i świadomie stosowany topos reductio ad impossibile, czyli dowód niewprost (w różnych wersjach). Popularne jest przypisywanie jego wynalazku Zenonowi Eleacie, nam wydaje się znacznie prawdopodobniejsze, że miast Zenona należy tu wymienić Melissosa Samijczyka (vide supra). Jeżeli nawet doda się do tego modus ponens (regułę odrywania) i przechodniość implikacji (zdaniowy sylogizm hipotetyczny), to nadal są to zaledwie trzy toposy, a więc w żadnym wypadku nie system (nawet minimalny). Dlatego wszelkich ewentualnych zależności szukać będziemy w rachunku nazw (sylogistyce).

Szukając zależności zajmijmy się najpierw wielkościami mierzalnymi. Ponieważ nie wiadomo, jakich wartości należałoby się spodziewać dla próbki losowej, będziemy mogli cokolwiek jednoznacznie stwierdzić jedynie w przypadku bardzo wyraźnych nieregularności.

Wyraźnym argumentem przeciwko istnieniu systemu minimalnego jest znaczna różnorodność stosowanych reguł, a zwłaszcza dobór funktorów: w sylogistyce klasycznej (nawet po dopuszczeniu łańcuszników i sylogizmów z wnioskiem warunkowym) mieści się niewiele ponad połowa wszystkich reguł nazwowych. Brak jest np. śladu konsekwencji w rozróżnianiu rozmaitych znaczeń słowa „jest”, oznaczanych dzisiaj przez ∈, ∋, ⊂, ⊃, ⊆, ⊇, =, ∦, podczas gdy Arystoteles używa (przynajmniej najczęściej) bardzo wyraźnego określenia „P przysługuje każdemu/jakiemuś S”. Wprawdzie inne funktory nie są bardzo popularne, nie jest to jednak ilość zaniedbywalna i ich częstość występowania nie odstaje rażąco od innych.

Jeśliby mówić o jakichkolwiek toposach sylogistycznych, to mogłyby to być najwyżej przechodniość relacji orzekania „A jest B” (czyli reguły, w których występuje wyłącznie inkluzja, identyczność lub przecinanie: ⊆, = lub ∦), stanowiąca dla wszystkich grup tekstów 38,1% wszystkich reguł nazwowych (127 z 333), zaś dla samych tekstów sokratycznych 41,6% (112 z 269). Trudno jednak określać przechodniość relacji „A jest B” mianem toposu, jako że nie wydaje się, by trzeba było jakiegokolwiek przygotowania do dokonania takiego rodzaju inferencji.

Spośród pozostałych reguł nazwowych brane pod uwagę mogą być jedynie wnioskowania postaci „jest, nie jest, nie jest” (czyli celarent i cesare z przestawionymi przesłankami oraz camestres z kolejnością przesłanek tradycyjną); jednak fakt, że większe znaczenie ma tu położenie przeczenia niż układ terminów wskazuje, że gra tu rolę jakiś efekt psychologiczny, a nie schemat logiczny.

Kolejnym argumentem przeciwko przyjęciu istnienia systemu minimalnego jest brak wyodrębnionego systemu sylogistycznego: argumenty sylogistyczne mieszają się z pozalogicznymi, brak jest spodziewanej konsekwencji, a jej miejsce zajmuje przypadkowość. Stąd niewiele argumentów (dowodów) jest zrekonstruowanych w całości; najczęściej fragmenty logiczne są jedynie przypadkowymi urywkami większych dowodów, w których pozatym nie stosuje się logiki.

Nieregularności w formie językowej są znacznie trudniejsze do określenia ilościowego, uwagi na ich temat są też bardziej subiektywne.

W pracy nad formalizacją dowodów przedarystotelesowych rzuca się w pierwszym rzędzie często odległy związek między surowym tekstem a jego — najbliższą nawet — formalizacją. Trudno jest uwierzyć, że autorzy mogli najpierw opracować dowód w postaci logicznej, a potem dopasować go do formy literackiej utworu, przybierając rozmaitymi ozdobnikami. Rzadko można na pierwszy rzut oka zorientować się w dłuższym fragmencie, które ze zdań jest istotne dla dowodu, a które są tylko dodatkami. Czasem trzeba było kilka dni poświęcić jednemu fragmentowi, aby skutecznie oddzielić wypowiedzi istotne od nieistotnych.

Taki sam wniosek daje porównanie wysłowienia poszczególnych wierszy w tym samym dowodzie (w tekście surowym, z którego wyciąg jest dołączany do formalizacji w t. II). Przede wszystkim widać, różne formy gramatyczne (osobowe, nieosobowe, abstrakcyjne) w tym samym dowodzie, typu: „dobro jest pożyteczne, pożyteczni jesteśmy dzięki cnocie, cnotliwi ludzie są mądrzy, więc dobro to mądrość”. Odnosi się to także do warstwy leksykalnej: używa się zamiennie synonimów (często niedokładnych), widać że zrozumienie czym jest błąd czterech terminów byłoby dla prearystotelików bardzo ciężkie.

c) głęboka analiza rozumowań

To co powiedzieliśmy dotąd, odnosi się do systemu minimalnego jako zbioru wzorcowych lub schematycznych rozumowań, które można było bezpośrednio przenieść na papier. Można jednak jeszcze przyjąć istnienie systemu logicznego jako techniki myślenia, rozumowania, której obraz na piśmie byłby jedynie wtórny. Stosując terminologię Chomsky’ego można zapytać, czy logika nie kryła się w „warstwie głębokiej”.

Do tak postawionego problemu należałoby podejść w zupełnie inny sposób. Zamiast badać zachowane teksty, należałoby rekonstruować rozumowania, które znalazły odbicie w tekstach — badać intencje autorów, a nie ich wyraz. Takie badania są prowadzone. Co więcej — były prowadzone już w starożytności.

Badań tych jednak nie da się wykorzystać w historii logiki: po pierwsze każdy badacz stosuje w nich tę logikę, która jest mu najlepiej znana, a w szczególności nowoczesną na jego czasy, po wtóre możliwa jest znaczna ilość formalizacji dowolnego wywodu i bardzo rzadko dochodzi do consensusu w sprawie uznania jakiejś formalizacji za najlepszą.

Mamy więc dylemat:

1. prowadzimy badania z historii dziedziny, do której należy rozważane rozumowanie (w szczególności historii filozofii); celem naszym jest zachowanie adekwatności merytorycznej; wykorzystujemy do tego całą dostępną sobie współczesną logikę; grozi nam tu zarzut anachroniczności metody, ale trzymamy się blisko intencji autora;
2. prowadzimy badania z historii logiki starożytnej, a wtedy narażamy się na zarzut „ślizgania się po powierzchni” i pomijania meritum.

Gdyby się okazało, że logika wystarczająca do adekwatnej formalizacji jakiejś dużej grupy argumentów (co byłoby ustaleniem historyka dyscypliny szczegółowej) pokrywałaby się z logiką znaną w czasie ich powstania (ustaloną przez badania historyka logiki), byłoby to doniosłym odkryciem empirycznym. Jednak z braku zajścia jakiegoś faktu historycznego nie można jednak czynić zarzutu historykowi. Nie jest winą historyka logiki, jeżeli jego badania nie wnikają w treść argumentacji — jeżeli tak jest, to jest skutek faktu historycznego: logika znana w czasach powstania danego argumentu nie wystarczała do jego ścisłego wyrażenia lub autor tego argumentu nie chciał jej stosować. Stwierdzenie tego faktu samo z siebie należy do zadań historyka.

d) wnioski

Tak więc możemy przyjąć za udowodnione (niewprost) twierdzenie:

Wniosek 1. Jeżeli zachowane teksty prearystotelików są reprezentatywne dla tego okresu, to przed Arystotelesem nie był znany żaden system logiczny porównywalny z jego sylogistyką

Niestety, nie da się uniknąć poprzednika tej implikacji: nigdy się nie dowiemy, czy w tekstach niezachowanych nie było niczego takiego.

Nie możemy też wykluczyć możliwości, że system minimalny istniał przed Arystotelesem, ale nikt go nie używał, albo ślady tego użycia się nie zachowały. W tym momencie jesteśmy zdani jedynie na zgadywanie: nie możemy i nigdy nie będziemy mogli ocenić czegoś, po czym nie został żaden ślad. Możemy tylko mieć nadzieję, że gdyby coś takiego było, to Arystoteles napisałby o tym, a neoplatońscy komentatorzy (niechętni Arystotelesowi) z radością by mu to wytknęli.

Możemy powiedzieć tyle:

Wniosek 2. Teza Arystotelesa o jego pierwszeństwie w sformułowaniu systemu logicznego nie da się sfalsyfikować.

Z drugiej jednak strony możemy trochę ograniczyć pojęcie reprezentatywności do środowiska, do którego należał Arystoteles: sokratyków. Wtedy z dużym prawdopodobieństwem można przyjąć kolejne twierdzenie:

Wniosek 3. Sokratykom nie był znany żaden system logiczny, porównywalny z sylogistyką Arystotelesa

Przez „nie był znany” należy tu rozumieć: „nie był przedmiotem rozważań ani stosowania”; nie można bowiem wykluczyć, że słyszeli o nim lub zetknęli się z przykładem jego stosowania (czego przykładem mogliby być np. Eutydem i Dionizodoros, z którymi spotyka się Sokrates w Eutydemie Platona).

1.2. Czy był ktoś, kto pierwszy używał logiki?

a) wszyscy ludzie?

Skoro przed Arystotelesem nie było nawet systemu minimalnego, to może mamy sytuację odwrotną: nikt nie odkrył logiki, bo wszyscy ją znają od urodzenia, wszyscy ludzie w sposób naturalny posługują się logiką

Jest to pogląd, z którym często się można spotkać; jest on także ukryty w poglądach, że logika odkrywa uniwersalne prawa myślenia.

Wyniki naszych badań zdają się temu przeczyć: poza pismami filozoficznymi logiki się prawie nie używa. Jak już podałem, w tekstach filozoficznych zawartych w corpus jedno użycie reguły logicznej przypada na 8 stron (licząc po 2000 znaków na stronę), a po odliczeniu Praw i Rzeczypospolitej (poza jej I księgą) Platona i Cyropedii Ksenofonta nawet na 5,7 strony, zaś w tekstach pozafilozoficznych raz na 215 stron, natomiast po odliczeniu krótkich utworów teoretycznych Hipokratesa i Antyfonta — nawet raz na 542 strony (dokładnie: 11 razy na 5962 stronach).

Możemy zatem odrzucić tę hipotezę i przyjąć następujące twierdzenie:

Wniosek 4. Przed powstaniem filozofii używanie logiki było jedynie akcydentalne.

b) wszyscy filozofowie?

Skoro tak, to postawmy hipotezę następującą: logika jest rówieśnicą filozofii.

Z utworów filozoficznych do końca V w. p.n.e. zachowały się tylko urywki, głównie jako cytaty w dziełach późniejszych. Zebrał je wszystkie i krytycznie opracował H. Diels w XIX w., a po jego śmierci uzupełnił W. Kranz w r. 1922. Cały zbiór Dielsa mieści się w dwóch tomach formatu B5 (tom III zawiera wyłącznie indeksy). Jest to wprawdzie prawie 900 stron, jednak tylko około jednej czwartej to teksty presokratyków: reszta to wspomnienia o nich, starożytne streszczenia ich utworów, oraz tłumaczenie niemieckie i aparat krytyczny.

W Dodatku 1. zamieściliśmy znalezione u presokratyków zastosowania logiki formalnej. Jest ich razem 51: prawie dwa razy więcej niż we wszystkich dziełach pozafilozoficznych corpus prearistotelicorum. 13 z nich zawartych jest we fragmentach Zenona i Melissosa Eleatów, 19 w dwóch utworach Gorgiasza: Pochwale Heleny i Obronie Palamedesa, zaś 15 w utworze nieznanego autora (prawdopodobnie sofisty) zaczynającym się od słów Dissoi logoi (Mowy podwójne, lub Dwojakie twierdzenia). Cała pozostała reszta to 4 zastosowania reguł logicznych (u Hippona, Filolaosa, Anaksagorasa i Diogenesa z Apollonii).

Na 895 stron zajmowanych u Dielsa przez presokratyków, fragmenty tych dwóch Eleatów zajmują 29 stron, cały Gorgiasz 36 stron (wymienione utwory — 15), a Dissoi logoi 12 stron. W sumie dwaj eleaci, Gorgiasz i Dissoi logoi zajmują więc 77 stron, czyli dwunastą część całości. Tak duża dysproporcja pozwala nam na konstatację:

Wniosek 5. Jeżeli fragmenty presokratyków są dla nich reprezentatywne, to poza Eleatami i niektórymi sofistami nie używali oni logiki

Na zakończenie rozważań o ogóle presokratyków należy jeszcze przestrzec czytelnika, że presokratycy to „motley band”, „przypadkowa zbieranina” jak ich nazywa J. Barnes, a to, że traktujemy ich jak spójną całość, to tylko skutek naszego przyzwyczajenia.

Jak wygląda zachowana logika Eleatów i sofistów? Zachowana logika Eleatów to głównie logika zdań, a zwłaszcza dowodzenie niewprost. Na 13 użytych przez nich reguł 7 to wnioskowanie niewprost, a 3 to reguła odrywania. Widać to też w ewidentnie będącym pod ich wpływem fragmencie platońskiego Parmenidesa 137c4–142a6 (u nas jako fr. 53), gdzie na 47 zastosowań reguł logicznych 7 to wnioskowania niewprost (we wszystkich innych tekstach Platona jest ich 18), a 6 to reguła odrywania (we wszystkich innych tekstach Platona reguł czysto implikacyjnych jest 10).

Logika dwóch mów Gorgiasza to także prawie czysty rachunek zdań (15 z 19 przypadków, przy czym z czterech pozostałych trzy są mieszane, nazwowo-zdaniowe, a tylko jedna jest czysto nazwowa). Tutaj już wnioskowanie jest bardziej zawiłe, a tylko 2/15 stanowią reguły czysto implikacyjne, zaś 4/15 wnioskowania niewprost. Być może jednak Gorgiasz posługiwał się także rachunkiem nazw, o czym świadczy forma dowodów użytych w przypisywanych Hipokratesowi utworach O sztuce i O naturze ludzkiej, które są wzorowane (jak się wydaje) na utworach Gorgiasza pod tymi samymi tytułami.

Z pewnością rachunkiem nazw posługiwał się autor utworu Dissoi logoi. Używa on reguł logicznych 15 razy, z tym że są to wyłącznie reguły nazwowe zawierające w sobie funktor „=". Wszystkie zresztą zrobione są wedle tego samego wzorca: autor stara się obalić twierdzenia, że tym samym jest dobro i zło, piękno i brzydota, prawda i fałsz etc. Z tych identyczności wyprowadza wnioski absurdalne. Ponieważ argumenty są niemalże identyczne, nie da się niczego powiedzieć o inwencji ich autora i jego ogólnej wiedzy logicznej.

Na pytanie, czy Eleatom, Gorgiaszowi bądź autorowi Dissoi logoi znany był system logiczny porównywalny z sylogistyką Arystotelesa, należy jednak odpowiedzieć:

Wniosek 6. Jeżeli zachowane teksty eleatów, Gorgiasza i autora Dissoi logoi są dla nich reprezentatywne, to żaden z nich nie posługiwał się logiką nazw na większą skalę, niż nie-filozofowie.

Wniosek 7. Jeżeli zachowane teksty Zenona, Melissosa i Gorgiasza są dla nich reprezentatywne, posługiwali się oni dość sprawnie podstawami klasycznego rachunku zdań i nie da się wykluczyć, że znali pewne zbiory ważnych reguł logicznych.

Są pewne przesłanki za tym, że inni sofiści mogli posługiwać się sylogistyką: Platon w Eutydemie opisuje dwóch braci, Eutydema i Dionizodora, którzy bardzo wprawnie posługiwali się sofizmatami sylogistycznymi. Jakieś światło na to mogłaby rzucić szczegółowa analiza Topik Arystotelesa. Nie da się jednak tej hipotezy zweryfikować.

c) Sokrates?

Kolejnym przedmiotem analizy są pisma sokratyków — Platona i Ksenofonta. Sokrates niczego nie pisał, a w każdym razie tradycja nic na ten temat nam nie przekazała (poza informacją o jego hymnie na cześć Apollina). Zachował się za to olbrzymi (równa jedna czwarta całego corpus prearistotelicorum) zbiór pism Platona — jego najsłynniejszego ucznia, oraz znaczne objętościowo pisma sokratyczne Ksenofonta i fragmenty innych sokratyków, wydane niedawno przez G. Giannantoniego. Jednym z sokratyków (uczniem Platona) był też Arystoteles.

Czy Arystoteles mógł skorzystać z dorobku Sokratesa?

Tak w młodzieńczych pismach Platona, jak i we wspomnieniach Ksenofonta Sokrates przeprowadza bardzo liczne dowody sylogistyczne. We wchodzących w skład corpus pismach sokratycznych reguły nazwowe stanowią 84% wszystkich zastosowań reguł logicznych (12% to reguły czysto zdaniowe, a 4% — mieszane). Wśród reguł zdaniowych połowa to wnioskowania niewprost, ćwierć to reguły czysto implikacyjne, a inne reguły zdaniowe oraz mieszane zdaniowo-nazwowe to tylko 23 z 322 wszystkich zastosowań reguł w tych tekstach. Porównanie sylogistyki Sokratesa z treścią Analityk pierwszych Arystotelesa czytelnik znajdzie tutaj, na razie ograniczę się do stwierdzenia:

Wniosek 8. Sokrates kompetentnie posługiwał się sylogistyką.

Wniosek 9. Sokrates prawie nie posługiwał się rachunkiem zdań.

Takie konstatacje potwierdzają wypowiedzi Arystotelesa z Metafizyki, zacytowane w Rozdz. II, zwłaszcza ta: „[Sokrates] słusznie szukał istoty. Szukał bowiem sylogistyki, zasadą zaś sylogizmów jest istota”.

Oba twierdzenia być może należy poprzedzić warunkiem „jeżeli pisma Platona i Ksenofonta dobrze opisują Sokratesa”. Pewnym uzupełnieniem byłoby tu przebadanie fragmentów tzw. „mniejszych sokratyków”. Badania nad dialogami pseudo-platońskimi nie ukazują znaczących różnic między późną tradycją sokratyczną a dialogami Platona.

Nie wiadomo, na ile fakt pojawienia się sylogistyki u Sokratesa był jego własną zasługą, a na ile był:

1. dziełem jego nauczycieli lub — ogólnie — środowiska intelektualnego Aten;
2. rezultatem tematyki, którą Sokrates się zajmował (poszukiwanie istoty cnót);
3. rezultatem stosowanej metody (krótkich pytań i odpowiedzi — rozbijania dyskusji na elementarne zdania, potwierdzane lub zaprzeczane).

W przypadkach b) i c) można też pytać o świadomość stosowania logiki (być może sama się narzucała), osobnym problemem jest, czy hipotetyczne przyczyny stosowania logiki (tematyka, metoda) były wynalazkiem Sokratesa, czy nie.

O tym, jak bardzo charakterystyczne dla Sokratesa było używanie sylogistyki, świadczy następujący przykład. W III księdze Cyropedii Ksenofonta, najstarszego romansu pedagogicznego, pojawia się znajome rozumowanie; młody Cyrus, król Persji, dowodzi królowi Armenii, że zasłużył na karę śmierci; dowód jest sylogistyczny (u nas fr. 28.). Czyżby Cyrus uczył się logiki? Ależ tak: pyta bowiem królewicza armeńskiego, Tigranesa, gdzież jest ów jego nauczyciel, z którym obaj przestawali w dzieciństwie. Tigranes odpowiada, że ojciec, król, skazał filozofa na śmierć za psucie mu syna. Mędrzec był jednak szlachetny i przyjął wyrok godnie; zabronił też Tigranesowi gniewać się na ojca, bowiem ów zrobił to z niewiedzy: nikt wszak nie czyni zła dobrowolnie…

d) Platon?

Czy był jakiś postęp w logice między Sokratesem a Arystotelesem?

Wniosek 10. Platon nie wniósł niczego do logiki.

Widzimy to patrząc na wykresy częstości użycia logiki w różnych okresach życia Platona (patrz tutaj). Najczęściej używał jej na początku, kiedy jeszcze dobrze pamiętał Sokratesa. Potem jest jej coraz mniej, a pod koniec nie ma jej prawie wcale (całe Prawa zawierają dwa tylko — i to bardzo elementarne — przykłady użycia logiki). Logika Platona nie różni się poza tym niczym szczególnym od logiki Ksenofonta. Nie wydaje się też, by inni sokratycy (starsi od Arystotelesa) znali w logice coś, co było nieznane Sokratesowi, a obecne u Arystotelesa.

W jednym tylko miejscu (fr. 53.) pojawia się logika innego rodzaju, ale tu z kolei Platon najprawdopodobniej czerpał od Eleatów (vide).

Wyrażano sugestie (np. Krońska [1985], ss. 86–87), że Platon pokazywał metodę Sokratesa w taki sposób, by ukazać jej bezowocność i nakłonić młodzież do studiowania w Akademii: Platon wyrażał pogląd (List VII 341b–345c, Fajdros 274c–275e), że prawdziwą wiedzę da się przekazać tylko przez obcowanie z mistrzem. Stąd znane uwagi wypowiadane przez platońskiego Sokratesa (np. w Teajtecie), porównujące go z położną mogą mieć charakter ironiczny — w istocie jego interlokutorzy nie są w stanie niczego urodzić. Przy takiej interpretacji obecności logiki u Platona jej brak w późniejszym okresie wydaje się zrozumiały: spełniła swoją rolę i Platon przestał jej potrzebować — nigdy bowiem nie potrzebował jej samej w sobie.

Wyjaśnienie faktu zmniejszania się częstości używania logiki u Platona nie należy do tematyki niniejszej rozprawy. Dla niej wystarczy stwierdzenie, że tak było, a zatem Sokrates nie musi dzielić się swym pierwszeństwem z Platonem.

Wiele szumu zrobiła sprawa rzekomego pochodzenia logiki Arystotelesa z metafizyki Platona, a w szczególności jego metody dychotomii (diairesis); sprawę tę omawiam wyżej.

1.3. Czy było coś, co narzucało używanie logiki?

a) matematyka?

Szeroko rozpowszechniony jest pogląd, że używanie logiki jest związane z dowodzeniem matematycznym. Tymczasem pogląd ten jest z gruntu błędny, i to tak w stosunku do logików starożytnych, jak i współczesnych.

W dowodach matematycznych także i dziś trudno znaleźć zastosowanie logiki: najczęściej matematycy dowodząc czegoś używają reguł matematycznych, tzn. takich, które nie są ważne na mocy samej logiki, ale zależą w sposób istotny od aksjomatów matematyki (w szczególności: arytmetyki). Nie eksplikują jednak tych aksjomatów, nie czują nawet zazwyczaj takiej potrzeby. O tym, czym jest dla matematyki logika, świadczy najlepiej historia formalizmu, czyli próby sprowadzenia całej matematyki do zbioru aksjomatów, na których operuje się regułami logicznymi. Jej celem nie było bynajmniej pokazanie, że dowody matematyczne to tylko niechlujnie przeprowadzone dowody logiczne, ale wskazanie niezachwianych podstaw, na których opiera się matematyka. Logika nie jest dla matematyka czymś, czego się używa, ale czymś, co daje pewność, że można bezpiecznie nadal używać tego, czego się i tak używało przed poznaniem logiki.

Czasami matematykowi zdarza się użyć jakąś regułę logiczną. Było też tak i u Euklidesa, i zapewne wcześniej (także przed Arystotelesem, choć nie mamy na to bezpośrednich dowodów). Tych przypadków u Euklidesa jest dość wiele, nie na tyle jednak, by odstawało to od normy dla dowodów w innych dyscyplinach nauk teoretycznych (w ówczesnym języku: filozofii). Nie ma też podstaw by uważać, że przed Euklidesem i Arystotelesem matematycy częściej używali logiki, a raczej przeciwnie: należy się spodziewać, że było jej jeszcze mniej niż u Euklidesa.

b) retoryka lub dialektyka?

Różnica między retoryką i dialektyką jest subtelna i łatwo je dziś pomylić. Obie mają za cel przekonywanie. Obie stanowią współzawodnictwo między (najczęściej dwiema) osobami przemawiającymi (z wyjątkiem retorycznych mów okolicznościowych). A jednak ogromnie się różnią co do użycia w nich logiki, a Arystoteles poświęcił im dwa osobne traktaty: retoryce Sztukę retoryczną, dialektyce Topiki: tylko te drugie wliczane są do pism logicznych (Organonu).

Najwyraźniejsza różnica między nimi to widownia, dla jakiej są przeznaczone: retorzy zwracali się do dużej grupy ludzi, tłumu na rynku bądź zgromadzenia ludowego (rady, sądu etc.), zaś dialektycy rozprawiali w wąskim gronie, np. w szkole. Druga różnica to długość wypowiedzi: mowa retora to kilka–kilkadziesiąt minut, a pojedyncza wypowiedź w dyskusji dialektycznej to jedno bądź kilka zdań.

W zachowanych mowach retorycznych znajdujemy tylko jeden przypadek użycia reguły logicznej, a mianowicie dość niewyraźne użycie sylogizmu celarent u Isokratesa. Tetralogie Antyfona, również zaliczane ze względu na ich autora do retoryki, są już właściwie dyskusją dialektyczną (co najwyżej czymś pośrednim). Żadnego dowodzenia logicznego nie znajdujemy też w licznych mowach wygłaszanych przez polityków, cytowanych przez Tukidydesa.

Taki stan w odniesieniu do retoryki, nie powinien dziwić: także dzisiaj trudno byłoby znaleźć posła lub dziennikarza używającego logiki w swych wystąpieniach.

Zupełnie inaczej działo się z dialektyką. W przeciwieństwie do retoryki, dialektyka nie zostawiła po sobie śladu w postaci zapisu wystąpień. Mamy kilka przykładów jej używania w dialogach Platona (np. Eutydem), w komediach Arystofanesa (np. Plutos, Chmury) mamy też traktat o niej, czyli Topiki Arystotelesa. Na tej podstawie odtwarza się, czym była grecka dialektyka. W swojej analizie posłużę się głównie znakomitym artykułem G. Ryle’a Dialektyka w Akademii Platońskiej, gdzie znajdujemy taki jej opis:

„What, then, is this exercise of dialectic, for which the Topics is a training manual? There is a special pattern of disputation, governed by strict rules, which takes the following shape. Two persons ‘agree to have a battle’. One is to be questioner, the other answerer. The questioner can only ask questions; and the answerer can, with certain qualifications, answer only ‘yes’ or ‘no’. So the questioner’s questions have to be properly constructed for ‘yes’ or ‘no’ answers. This automatically rules out a lot of types of questions, like factual questions, arithmetical questions, and technical questions. Roughly it leaves us only conceptual questions, whatever these may be. The answerer begins by undertaking to uphold a certain ‘thesis’, e.g. that justice is the interest of the stronger, or that knowledge is sense-perception. The questioner has to try to extract from the answerer, by a series of questions, an answer or conjunction of answers inconsistent with the original thesis, i.e. drive him into an ‘elenchus’. The questioner has won the duel if he succeeds in getting the answerer to contradict his original thesis, or else in forcing him to resign, or in reducing him to silence, to an infinite regress, to mere abusiveness, to pointless yammering, or to outrageous paradox. The answerer has won if he succeeds in keeping his wicket up until the close of play. The answerer is allowed to object to a question on the score that, for example, it is two or more questions in one, like have you left off beating your father?, or that it is metaphorical or ambiguous. The duel is fought out before an audience […] and apparently it is sometimes left to the audience to judge whether the questioner or the answerer has won. Certain debating tricks and manoeuvres are recognised as fouls. […] The exercise has to have a time-limit, or else the answerer can never win”.

Ryle podsumowuje swoje i swoich poprzedników studia następująco:

„Our study of the eristic or dialectical exercise has shown us something of what is going on in the Academy during the last ten or twelve years of Plato’s life and the first ten or twelve years of Aristotle’s teaching life. Eristic contests have become a part of the curriculum even for fairly junior members of the Academy, and both Plato and Aristotle are keenly interested not only in its gymnastic utility but also in its philosophical productiveness, in our sense of ‘philosophical’. Aristotle’s pedagogic interest in the Art of constructing and rebutting elenchi leads him into the pure theory of valid versus fallacious argument, but only at a later stage. The idea of Confutation-without-cheating precedes the idea of validity”.

Wiemy już, czym była dialektyka i że — być może — z niej zrodziła się logika, choć była do niej droga dość daleka. Czy jednak dialektycy przed wstąpieniem Arystotelesa do Akademii posługiwali się regułami logicznymi?

Wielu osobom przypisywano bycie pierwszym dialektykiem; najpewniej praktyka ta powstała wśród ludzi z generacji urodzonej między ok. 490 a ok. 470 r. p.n.e., takich jak Zenon z Elei, Melissos, Protagoras, Antyfon Retor i Sokrates. Ustaliliśmy już, że ponad wszelką wątpliwość Sokrates wprawnie posługiwał się logiką. We wcześniejszych tekstach (poza paru tylko wstawkami u Herodota) nie znajdujemy jej. Można więc co najmniej uznać, że początki stosowania logiki były równoczesne z pojawieniem się zawodów dialektycznych.

Autorzy późniejsi, u których natrafiamy na używanie logiki (Platon, Ksenofont), byli uczniami Sokratesa i znali jego metodę. Nie da się więc jednoznacznie wykluczyć, że ci, którzy praktykowali pojedynki dialektyczne, posługiwali się logiką, choć należy tu być bardzo ostrożnym, bo taka zbieżność może być po prostu rezultatem braku innych źródeł. Zależność w drugą stronę, że dialektyka była jedynym sposobem używania logiki przed Arystotelesem, nie może być utrzymana, bo znajdujemy przypadki jej zastosowań w tekstach nie mających bezpośredniego związku z dialektyką. Wśród wszystkich tych przypadków zachodzi jednak unia personalna: o osobach tych skądinąd wiemy, że zajmowały się dialektyką, z wyjątkiem może Melissosa (choć Zenon zapewne był dialektykiem) i matematyków (choć tu możemy tylko stypulować, bo przedarystotelesowe dowody matematyczne się nie zachowały, a z drugiej strony nie da się wykluczyć, że matematycy też organizowali takie zawody). Taki związek może być jednak rezultatem czystego przypadku i wydaje się, że zależności w tę stronę nie było.

c) filozofia?

Wszystkie prawie ślady użycia logiki pochodzą od osób zajmujących się badaniami teoretycznymi, zwanymi wówczas filozofią, lub pojawiają się jako cytaty z wypowiedzi takich osób. Nie wiadomo, czy to dlatego, że takie właśnie osoby ćwiczyły się w dialektyce, traktowanej jako propedeutyka filozofii, czy też była to zależność odwrotna: tylko teoretycy posługiwali się logiką, a wtórną rzeczą było, że skądinąd tacy właśnie ćwiczyli dialektykę. Nie używali logiki lekarze (Corpus Hippocraticum poza pismami filozoficznymi), historycy (tylko Herodot, i to z rzadka), retorzy (vide punkt poprzedni) ani epicy. Dramaturdzy używali jej z rzadka, robiąc aluzje do dysput filozofów.

Być może pewna tematyka filozoficzna miała wpływ na użycie logiki, mianowicie Sokratesowe poszukiwanie istoty cnót. Szukając istoty, musiał — jak się wydaje — zejść wgłąb definicji, używać logiki rozbijającej zdanie na definiens i definiendum, a więc logiki nazw. Tak sugeruje wypowiedź Arystotelesa z Metafizyki (vide).

2. Podobieństwa i różnice między logiką Arystotelesa i logiką stosowaną przez jego poprzedników

Czym różniła się więc logika stosowana przed Arystotelesem od logiki opisywanej przez niego? Zdefiniujmy najpierw, co będziemy nazywać logiką Arystotelesa (dalej: LA) i logiką prearystotelików (dalej: LPA).

Za LA przyjmujemy to, co jest wyłożone w Analitykach Pierwszych. W zachowanych pismach Arystotelesa nie ma niczego wychodzącego w logice poza Analityki Pierwsze. Zapewne było coś w pismach Teofrasta i Eudemosa, pisanych być może jeszcze pod kierunkiem Arystotelesa, nie były one chyba jednak sprzeczne z treścią Analityk Pierwszych (poza, być może, elementami logiki modalnej Teofrasta). Nie wnikam tu w problematykę tego, czy sylogizmy Arystotelesa są prawami implikacyjnymi czy regułami dedukcji naturalnej; logicznie jedne są równoważne drugim, a sam Arystoteles zapewne nie zdawał sobie sprawy z tego rozróżnienia lub nie uważał go za istotne.

Za LPA przyjmujemy to, co odnaleźliśmy w pismach prearystotelików. Być może pisma te nie są reprezentatywne, ale nic innego nie mamy i mieć nie będziemy, musimy więc wziąć je za dobrą monetę. Z formalnego punktu widzenia LPA są to wszystkie odnalezione reguły. Zbiór ten nie jest domknięty ze względu na konsekwencję (znajduje się w nim tylko to, co zostało znalezione); co więcej — jest on zbiorem rozmytym: przynależność do niego możemy stopniować w zależności od częstości występowania danej reguły (możemy wyróżnić LPA par excellence i jej obrzeża).

W kilku sensach można mówić o tym, że LA była rozwinięciem lub uproszczeniem LPA. Co za tym idzie, w kilku sensach możemy mówić, że Arystoteles dołożył coś do LPA lub od niej coś odjął.

W najpełniejszym z tych sensów możemy o tym mówić, jeżeli zgodzimy się na następujące założenie: Arystoteles przeprowadził gruntowne badania nad używaniem logiki. Argumentem za tym jest istnienie Topik oraz fakt, że najprawdopodobniej niczego podobnego do Topik przed Arystotelesem nie sporządzono (byłby to system minimalny, którego istnienie wykluczyliśmy powyżej), a więc Arystoteles osobiście musiał się z LPA zapoznać. Jeżeli tak, to LPA była znana Arystotelesowi: dysponował zbiorem reguł, wyabstrahowanych z praktyki dialektycznej; jeżeli się na to zgodzimy, to porównanie LPA z LA ukaże nam świadomy wkład Stagiryty: co zmienił w logice zastanej, co dodał, co opuścił.

Nie zgadzając się na to założenie (to znaczy stwierdzając, że badania Arystotelesa nie były tak gruntowne, by mógł on na ich podstawie mieć w miarę pełen obraz LPA), możemy jeszcze przyjąć, że LPA była — przynajmniej dla Arystotelesa i jego środowiska — logiką naturalną. Więc jeśli nawet odrzucimy hipotezę, że Arystoteles świadomie ją badał, nasze zestawienie może nam ujawnić, czy intuicja Arystotelesa, by sformalizować najpierw takie, a nie inne obszary logiki, była trafna (przy założeniu znowu, że Arystoteles chciał sformalizować logikę stosowaną).

Odrzuciwszy także to założenie, a więc stwierdzając, że Arystotelesa nie interesowało formalizowanie logiki stosowanej, że tworzył on swój system zupełnie od podstaw, teoretycznie, nadal możemy porównywać obie logiki jako byty z Popperowskiego Trzeciego Świata, teorie w sensie idealnym, niezależne od ich autorów; tak porównywać można dowolne dwa systemy logiczne.

Którego z powyższych sensów zwrotu „dołożyć coś do logiki prearystotelików” będziemy używać, jest w poniższych rozważaniach nieistotne; wybór jednego z nich umożliwi stosowną interpretację wyników, a nie samo ich ustalenie.

2.1. Zdanie kategoryczne: opozycja liniowa czy kwadrat logiczny?

Zdanie proste w LA (niezależnie czy asertoryczne, czy modalne) może być w jednym z sześciu rodzajów: ze względu na kwantyfikację może być ogólne (dosł.: całościowe — katholou), szczegółowe (dosł.: częściowe — en merei) lub niepoliczalne (adioristos); bez względu na nią może być twierdzące lub przeczące.

Tymczasem w LPA mamy prawie wyłącznie zdania niepoliczalne. Rozważań, w których zaszłaby konieczność kwantyfikacji, prowadzi się bardzo mało. Naturalną postacią zdania jest zdanie o podmiocie w liczbie pojedynczej (jego podmiotem jest jakaś rzecz lub pojęcie: zbiór kolektywny, np. „człowiek” w zdaniu „człowiek jest śmiertelny”). Zdanie takie jest zarazem konieczne i ogólne: wyraża prawdę uniwersalną, np. twierdzenie naukowe. System taki nie umożliwia rozróżnienia sprzeczności i przeciwieństwa: oba są utożsamione z negacją zdania prostego (zdanie „nieprawda, że człowiek jest rybą” jest równoważne zdaniu „człowiek nie jest rybą”). Dopóki podmiot zdania miał supozycję jednostkową (oznaczał indywiduum, zbiór kolektywny lub klasę abstrakcji, czyli jednym słowem był teoriomnogościowym atomem), nie prowadziło to do błędów. Ale logika taka nie pozwalała na traktowanie podmiotu jako zbioru dystrybutywnego. Taka logika panuje jeszcze w Topikach Arystotelesa (Kneale [1962], ss. 37–40).

Z kolei w LA negacja ogólnego zdania twierdzącego nie jest tym samym, co ogólne zdanie przeczące (resp. „nie każdy człowiek jest rybą” i „każdy człowiek nie jest rybą”). Arystoteles przeprowadził rozróżnienie pomiędzy sprzecznością i przeciwieństwem i dodał do liniowej opozycji przeciwnych zdań ogólnych (twierdzące — przeczące) ich negacje, tworząc kwadrat logiczny. Nie dość, że umożliwił dowodzenie za pomocą zdań o zbiorach dystrybutywnych (policzalnych), ale prawie zupełnie zrezygnował z zajmowania się innymi.

Badania teoretyczne nad formą zdania (semantyczne i gramatyczne) są przedstawione w Hermeneutyce. Być może Arystoteles prowadził je jeszcze pod kierunkiem Platona. Wydaje się więc, że tym, co Arystoteles wniósł nowego do logiki, była decyzja wyboru, spośród różnych możliwych typów zdań, właśnie zdań kwadratu logicznego. Owo połączenie LPA i zależności kwadratu logicznego jest podstawą LA. Na tym tle dość dobrze uzasadniona wydaje się hipoteza É. de Stryckera o częściowym pochodzeniu sylogistyki z platońskiej teorii całości i części. Arystoteles raczej nie mógł wziąć przeciwstawienia zdania „całościowego” (katholou, w tradycji łacińskiej zwanego „ogólnym”) i „częściowego” (en merei, w tradycji łacińskiej zwanego „szczegółowym”) z LPA, bo go w niej nie ma. Nie ma go też w diairesis Platońskiej. Jednak podstawowym miejscem, gdzie Arystoteles zajmuje się teorią zdania jest Hermeneutyka, więc szczegółowe badanie tej kwestii stoi poza obszarem naszych obecnych badań i pozostawiamy je komentatorom Hermeneutyki.

2.2. Modalności: ilość i jakość

Arystoteles uczynił też inną dystynkcję: oddzielił modalności aletyczne od kwantyfikacji. W LPA modalność (zazwyczaj konieczność, z wyjątkami, o których niżej) tkwiła in re, nie było potrzeby jej eksplikacji: jeżeli a) męstwo jest cnotą, to b) każdy czyn mężny jest czynem cnotliwym oraz c) konieczne jest, że każdy czyn mężny jest czynem cnotliwym (bo jeśli męstwo jest cnotą, to do istoty czynu mężnego należy bycie czynem cnotliwym). Arystoteles rozróżniając b) i c) pozwolił na rozróżnienie zdań ogólnych na przygodne — empiryczne i istotne — naukowe (co było istotną częścią jego teorii nauki, wyłożonej zwłaszcza w Analitykach wtórych). Nie dopracował swej teorii sylogizmów modalnych do końca, ale wystarczającym osiągnięciem było oczyszczenie kwantyfikacji z intensji koniecznościowej. Wprawdzie dopiero Ockham na dobre przeniósł konieczność z rzeczy (konieczność metafizyczna) do zdań (konieczność logiczna), ale przygotowane to zostało przez Arystotelesa.

Modalność u prearystotelików może być wyrażana rozmaicie. Zdanie ogólne nie wymaga żadnych dodatków: każde zdanie, jeżeli nic nie stoi na przeszkodzie, jest ogólne. Zdanie szczegółowe występuje w szczególności w kontekstach hipotetycznych, zwłaszcza związanych z dowodzeniem niewprost („gdyby chociaż jeden x był A…”), sytuacjami kontrfaktycznymi i okresami warunkowymi. Modalność u prearystotelików bywa wyrażona ilościowo (kwantyfikacja): „wszystkie”, „jakieś”, „niektóre”, modalnościami aletycznymi: „na pewno”, „z pewnością”, „być może”, „koniecznie”, „możliwe, że…”, epistemicznie: „wiadomo”, „nie wiadomo”, określeniami temporalnymi: „zawsze”, „w każdym przypadku”, „czasem”. Określenia te mogą pojawiać się explicite, ale częściej można się ich domyślić z kontekstu.

2.3. Funktory od argumentów nazwowych (funktory nazwowe)

Cztery funktory sylogistyki asertorycznej Arystotelesa wystarczą do sformalizowania większości przedarystotelesowych dowodów czysto nazwowych. Nie jest to jednak większość przytłaczająca: 53% wszystkich zastosowań reguł nazwowych tu analizowanych (tj. w corpus, we fragmentach presokratyków i w dialogach pseudoplatońskich) a 58% w pismach sokratyków. Spośród pozostałych 155 (resp. 113) zastosowań reguł, stanowiących 47% (resp. 42%), 125 (88), czyli 81% (78%) to reguły, do których formalizacji potrzeba dołączenia przynajmniej jednego z pięciu funktorów nazwowych: dwóch zdaniotwórczych — identyczności (=) i nieidentyczności (≠) — i trzech nazwotwórczych — negacji/dopełnienia (¬), koniunkcji/iloczynu (∩) lub alternatywy/sumy (∪). Reszta, czyli 30 (25) to reguły z funktorami specyficznymi, zwane od starożytności sylogizmami o terminie w przypadku zależnym (a recto ad obliquum, dosł.: „od [terminu] w przypadku niezależnym [tj. w mianowniku] do [terminu] w przypadku zależnym”), z których część także wykorzystuje któryś z tych dodatkowych pięciu funktorów.

Arystoteles w Analitykach Pierwszych pisze o większości tych dodatkowych funktorów — był ich świadom, ale zapewne dla prostoty nie zajął się nimi; bardziej zajmowały go sylogizmy modalne. W rozdziale 39. pisze o tożsamości, którą rozumie jako stwierdzenie zastępowalności jednego terminu przez drugi — dlatego nie jest ono traktowane jako przesłanka sylogistyczna. W rozdziale 36. pisze o sylogizmach z terminem w przypadku zależnym, sprowadzając je do zwykłych sylogizmów. W rozdziale 40. zaś o negacji przynazwowej. Jedynie wiec suma i alternatywa nazwowe zostały przez Arystotelesa pominięte i do sylogistyki włączył je w pełni dopiero August De Morgan.

2.4. Rachunek zdań

Zdaniem Łukasiewicza wielkim niedostatkiem Arystotelesa było nieuwzględnienie przezeń logiki zdaniowej, która jest podstawą wszelkiej logiki, w tym i sylogistyki. Jak wyglądały przedarystotelesowe dowody logiczne opierające się na logice zdań?

Mimo zastrzeżeń wobec ostrego rozgraniczenia logiki nazw i logiki zdań, musimy się zgodzić, że w przypadku LPA podział taki ma uzasadnienie. Stosunkowo mało jest reguł, w których występują zarówno funktory od argumentów zdaniowych, jak i od nazwowych. Zazwyczaj wnioskowania zdaniowe występują w jednym z dwóch kontekstów: albo prowadzi się dowód zdaniowy, nie wchodząc w zależności między terminami (tak jest często poza tekstami sokratyków), albo rachunku zdań używa się metasystemowo. Tak u Arystotelesa, jak i u przedarystotelesowych sokratyków dowody zdaniowe mają charakter najczęściej metasystemowy, znajdują się w obrębie dowodów sylogistycznych, ich przesłanki są dowodzone sylogistycznie, a konkluzja bywa przesłanką do innych sylogizmów; często (zwłaszcza w dowodach niewprost) nie pojawia się żaden funktor zdaniowy.

Zdecydowanie na pierwszym miejscu wymienić należy wszelkiego rodzaju przypadki dowodzenia niewprost. Razem stanowią one 50% wszystkich zanalizowanych użyć reguł zdaniowych (51% u sokratyków), Do tej kategorii zaliczone zostały: kontrapozycja (2%, u sokratyków 0%), reguła dowodzenia niewprost (37%, resp. 26%), dowód niewprost (11%, resp. 26%). Mianem kontrapozycji została tu określona reguła „p→q ⊢ ~q→~p”. Reguła dowodzenia niewprost powstaje przez przesunięcie poprzednika konkluzji kontrapozycji do zbioru jej przesłanek: „p→q, ~q ⊢ ~p”. Dowód niewprost z kolei powstaje, jeżeli zamiast zakładać w regule dowodzenia niewprost implikację p→q, pokazujemy, że q da się udowodnić przy założeniu p: „(p⊢q), ~q ⊢ ~p”. Większą różnorodność uzyskujemy przez permutowanie przesłanek i przestawianie znaku negacji (np. reguła dowodzenia niewprost może mieć kształt: „q, ~p→~q, ⊢ p”). Dalsze urozmaicenie osiąga się poprzez iterację tych reguł oraz dokładanie przechodniości implikacji. W jednym przypadku nie ma dowodu, wnioskiem jest tylko, że coś trzeba odrzucić, ale nie wiadomo co — oznaczyłem go jako absurd (⊥).

Najważniejszą obserwacją na ten temat jest fakt, że wśród reguł dowodzenia niewprost i dowodów niewprost 88% (resp. 95%) stanowią ich słabe wersje, czyli takie, których konkluzja jest zanegowana. Tylko w sześciu przypadkach na 50 (resp. w jednym na 20) dowodzi się w ten sposób formuły pozytywnej.

Dowody niewprost stanowią ważną część systemu sylogistyznego Arystotelesa. Służą one redukcji niektórych trybów do trybów figury pierwszej, toteż Arystoteles rozważa je w szczegółach (np. w rozdz. 29. księgi I. Analityk Pierwszych).

Poza sylogistyką stoją pozostałe reguły zdaniowe: reguły czystej implikacji (głównie reguła odrywania), stanowiące 23% (resp. 26%) wszystkich reguł zdaniowych i reguły pozostałe (28%, resp. 23%, w wielkościach absolutnych: 29, resp. 9), używające co najmniej jednego z funktorów zdaniowych: koniunkcji (∧), alternatywy (∨), alternatywy rozłącznej (⊻) i równoważności (↔). Jest ich zbyt mało, aby wyciągać na tej podstawie jakiekolwiek ogólne wnioski (poza tym właśnie wnioskiem, że jest ich mało).

2.5. Dowody przez ektezę

Kolejną rzeczą o której warto wspomnieć jest procedura ektezy. Arystoteles wprowadza ją w Analitykach Pierwszych jako trzeci rodzaj dowodu (poza dowodem przez reguły konwersji i reductio ad absurdum). Wydaje się, że polega ona na arbitralnym wskazaniu dowolnego indywiduum spełniającego jakiś warunek, po to by później (po przeprowadzeniu stosownej ilości operacji na tym elemencie) wrócić do zdania o terminach ogólnych, w oparciu o ową nieskrępowaną dowolność, z jaką indywiduum to zostało wybrane.

Nie udało się znaleźć u prearystotelików żadnego dowodu, w którym byłoby przejście ze zdania o terminach ogólnych do zdania o terminach szczegółowych, po to by znowu wrócić do terminów ogólnych. Dlaczego tak było — można snuć różne przypuszczenia. Być może taka operacja byłaby uznana za niestosowną (zbędne odejście od ogólności), być może była zbyt skomplikowana, być może wreszcie dlatego, że ektezą Arystotelesową nie da się udowodnić zdania ogólnego, a one zdecydowanie przeważają.

Ekteza gra natomiast niezwykle ważną rolę w matematyce. Każdy dowód Euklidesa możemy nazwać dowodem przez ektezę. Dowód taki składał się z sześciu części: protasis (cel ogólny), ekthesis (ekteza), diorismos (cel szczegółowy), kataskeue (konstrukcja), apodeixis (dowód właściwy), symperasma (podsumowanie). Ekteza to stwierdzenie postaci „niech AB będzie danym odcinkiem”. Mieści się ona między protasis („na danym odcinku skonstruować trójkąt równoboczny”) a diorismos („tak więc trzeba skonstruować trójkąt równoboczny na odcinku AB”).

Nie wiadomo, czy pod Arystotelesowym pojęciem ektezy kryło się to samo, co pod pojęciem ektezy matematycznej, wiadomo jednak, że Arystoteles znał ektezę matematyczną i nazywał ją tym właśnie słowem. Ponieważ nieprawdopodobne jest, by słowo „ekteza” było wprowadzone do matematyki przez Arystotelesa (nie zajmował się on czynnie matematyką, więc nie było powodu, by matematycy wykorzystywali jego terminologię) więc najprawdopodobniej znał je zanim jeszcze sformułował sylogistykę.

Ze zbieżności nazwy nie należy wyciągać zbyt daleko idących wniosków; zapewne Arystoteles użył tylko słowa będącego w powszechnym użyciu („wyróżnienie”) do określenia z grubsza podobnej procedury. Za tym, że Arystoteles zaczerpnął procedurę ektezy z matematyki przemawia głównie fakt jej braku (przeciwnie do pozostałej treści Analityk Pierwszych) w zachowanych tekstach prearystotelików.

3. Konkluzja: propozycja rekonstrukcji prehistorii logiki

Niniejszy szkic opiera się na ustaleniach poczynionych w rozdziale poprzednim. Nie wszystkie jednak fakty tu przedstawione dadzą się udowodnić, znaczna ich część na zawsze pozostanie kwestią subiektywnej oceny historyka. Przedstawiając kilkakroć publicznie problematykę zawartą w niniejszej pracy spotykałem się jednak zawsze z niecierpliwym pytaniem „jak to w końcu było naprawdę?” lub „jak mamy odpowiedzieć na egzaminie?” Staram się więc wyjść naprzeciw tym potrzebom, zapraszając zarazem do dyskusji osoby, które się z nie zgodzą z niżej przedstawionym opisem.

Wszystko wskazuje, że nasi przodkowie nie myśleli logicznie. Nie musiało im to bynajmniej przeszkadzać; problemy, przed jakimi stawali, nie wymagały logiki, by je rozwiązać. Nie mówię, że nie potrzebowali wiedzy logicznej, jak p. Jourdain nie potrzebował wiedzieć, że mówi prozą, by to robić; oni nie posługiwali się logiką: tak jak p. Jourdain nie mówił greką — podobnie jak jemu, nie była im do niczego potrzebna. Ogromna większość ludzi — zdaje się — żyje w ten sposób do dzisiaj, szkoła może mieć tu wpływ najwyżej marginalny, a przede wszystkim — krótkotrwały, nie jest bowiem w stanie (prawie nigdy) takiej potrzeby wzbudzić.

Podobnie, jak wiedza gramatyczna na temat własnego języka staje się potrzebna dopiero w sytuacjach wątpliwych, gdy intuicja native speakera zawodzi, tak też logika stała się potrzebna dopiero po pojawieniu się rozumowań, w których potoczna intuicja, common sense, zawodziła. Taką sytuacją było pojawienie się nauk teoretycznych, zwanych wówczas ogólnie filozofią.

Nie stało się to jednak od razu; do dzisiaj zresztą wiele osób mieniących się filozofami nie stosuje logiki w swej pracy. Musiało bowiem dojść do sytuacji, w której filozofowie zaczęli ze sobą dyskutować, przekonywać siebie nawzajem i innych. Aby więc powstała potrzeba użycia logiki, musiały się pojawić dyskusje teoretyczne.

Grecy bardzo lubili dyskutować; debaty ich jednak miały postać głównie przemówień wygłaszanych na rynku, w sądzie, na zgromadzeniu ludowym. W zapisanych mowach z tamtych czasów nie widzimy prawie śladów używania w nich logiki: aby przekonać tłum, należało posługiwać się zupełnie innymi środkami przekonywania: retoryką. Te mowy, w których logiki się używa, są w zasadzie skierowane wyłącznie do wąskiej grupy osób: do uczniów i przyjaciół; są mowami pozornymi, podręcznikowymi.

Rozważania teoretyczne też były wśród Greków dość popularne; dopóki miały jednak postać wyroczni, złotych myśli przypisywanych boskim mędrcom, nie było w nich miejsca na logikę.

W pewnym momencie te dwa nurty się przecięły. Zaczęto dyskutować o rzeczach ogólnych. Rozważania były oparte o rachunek zdań; Melissos dowodził, że byt nie może mieć wymiarów, bo gdyby był ograniczony, to by nie istniał, a przecież istnieje. Gorgiasz bronił Palamedesa w ten sposób, że tenże nie mógł spiskować przeciw Achajom, bo by ich zdradzić musiałby się spotkać z Trojańczykiem, by się z nim spotkać musiałby się z nim porozumieć, by się z nim porozumieć musiałby z nim rozmawiać, a to przecież niemożliwe, skoro Palamedes nie mówił po trojańsku; nie mógł więc zdradzić Achajów. By pochwalić Helenę Gorgiasz wykorzystywał rozbudowaną alternatywę czterech członów; ponieważ każdy z nich prowadzi do tej samej konkluzji, można ją przyjąć za udowodnioną.

Te argumenty przekonywały, nie dotykały jednak istoty rzeczy. Logika nie potrafiła wejść do wewnątrz zdania prostego i np. wyciągać z definicji wniosków o własnościach. I wtedy pojawił się Sokrates. Sokrates zaczął definiować; chodził po rynku, rozmawiał z ludźmi i pytał ich, czym jest cnota, czym męstwo, czym miłość, a czym sprawiedliwość. Później wyciągali wnioski: cnota jest dobra, a dobro to piękno — cnota musi więc być piękna. Ale przebiegłość nie jest piękna — nie może więc być cnotą.

Teraz dopiero logika zaczęła się panoszyć; gdzie tylko pojawia się Sokrates, pojawiają się takie właśnie rozumowania. W pismach jego uczniów (sam niczego nie zostawił) pojawiają się prawie wyłącznie takie właśnie dowody (vide). Można mieć wątpliwości, czy Sokrates był twórczym filozofem, nie można jednak wątpić, że w logice zasłużył się ogromnie większe zbiory pism (przynajmniej po nich pisma te się zachowały): Platon i Ksenofont. O ile jednak Ksenofont był raczej pamiętnikarzem niż filozofem, o tyle Platon przez wielu jest wciąż uważany za największego filozofa wszechczasów. Żaden z nich nie wniósł — jak się zdaje — twórczego wkładu w logikę; obaj tylko cytują Sokratesa, zapewne dość wiernie. Platon, gdy dojrzał, zaczął głosić własne poglądy i logika przestała być mu potrzebna. W jednym ze swoich utworów (Parmenides) umieścił długi dowód w konwencji zdaniowej, można jednak zasadnie wątpić, by był on jego autorstwa.

Wtedy pojawił się Arystoteles; wychowany w kulcie Sokratesa, stykał się przez wiele lat z jego logiką. Ponieważ był to prawie jedyny sposób uprawiania logiki, jaki był znany w jego środowisku, nic dziwnego, że to właśnie on stał się przedmiotem jego opracowania, gdy postanowił ująć go od strony teoretycznej. Zgromadził najpierw i usystematyzował przykłady wnioskowań (toposy w Topikach), a potem je uogólnił i powiązał w system (w Analitykach).

Tak odtworzyć można uproszczony schemat rozwoju logiki w jej początkowym okresie:

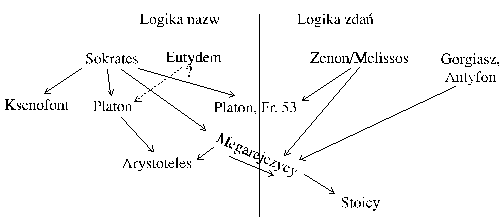
Po stronie logiki nazw prekursorem jest Sokrates — od niego wywodzą się wszystkie znane linie. Logika zdań ma kilku ojców: eleatów (Zenon, Melissos) i sofistów (Gorgiasz, Antyfon Retor). Ogniwami pośrednimi są eleacki fragment platońskiego Parmenidesa i szkoła megarejska, której założyciele byli sokratykami, ale dali początek zdaniowej logice stoików.

Tak wyglądały najprawdopodobniejsze losy logiki formalnej przed Arystotelesem.