Summary: The Pre-Aristotelian Formal Logic
Część I - Logika formalna przed Arystotelesem
- Wstęp
- Objaśnienia ważniejszych pojęć
- Wybrane dotychczasowe ujęcia przedarystotelesowej logiki formalnej
- Plan badań i metodologia
- Opis zgromadzonego materiału źródłowego
- Fragmenta praearistotelicorum — przykłady
- Analiza wyników
- Rozstrzygnięcia
- Bibliografia
Część II - Katalog przedarystotelesowych fragmentów logicznych
I. Fragmenta prearistotelicorum
- Układ pozycji katalogowej
- System przyjęty w formalizacji
- Reguły logiczne znalezione u prearystotelików
- Kanon pism prearystotelików
- Spis znalezionych fragmentów logicznych w pismach prearystotelików
- Katalog fragmentów logicznych znalezionych w pismach prearystotelików
- Dodatek 1.: fragmenty logiczne we fragmentach presokratyków
- Dodatek 2.: fragmenty logiczne w pismach pseudoplatońskich
Marek Jerzy. Minakowski, Prehistoria logiki formalnej
I. Fragmenta prearistotelicorum
3. Reguły logiczne znalezione u prearystotelików
Kolejność w ramach punktu:
- ilość przesłanek
- kolejność alfabetyczna zmiennych (w przesłankach): najpierw zmienne nazwowe (litery łacińskie), potem zdaniowe (litery greckie)
- kolejność funktorów (w przesłankach) według listy: ⊆, =, ∦, ¬, ∥, ⊈, ≠, ∪, ∩, →, ~, ∧, ∨, ⊻, ↔, ⊥, funktory specyficzne
- jeżeli układy przesłanek są identyczne, punkty 2. i 3. odnoszą się do wniosku
Po każdej regule podano numery fragmentów, w których występuje (jeżeli w jednym fragmencie pojawia się kilka razy, numer jest powtórzony stosowną ilość razy); numery fragmentów nie należących do kanonu (fragmenty presokratyków i pseudo-Platona) podano kursywą.
Typy reguł (liczby w nawiasie oznaczają ilość znalezionych reguł danego typu i ilość ich wystąpień)
I. Sylogistyka (rachunek nazw, predykatów)
1.1. Funktory jednego rodzaju (25, 101)
1.1.1. ⊆ (13, 84)
1.1.2. = (11, 16)
1.1.3. ∥ (1, 1)
1.2. Funktory dwóch rodzajów (46, 119)
1.2.1. ⊆ = (12, 21)
1.2.2. ⊆ ∦ (3, 4)
1.2.3. ⊆ ¬ (1, 1)
1.2.4. ⊆ ∥ (10, 64)
1.2.5. ⊆ ⊈ (3, 5)
1.2.6. ⊆ ∩ (6, 6)
1.2.7. = ¬ (3, 3)
1.2.8. = ∥ (4, 6)
1.2.9. = ≠ (1, 1)
1.2.10. ¬ ∥ (3, 8)
1.3. Funktory trzech rodzajów (39, 52)
1.3.1. ⊆ = ¬ (2, 2)
1.3.2. ⊆ = ∥ (1, 1)
1.3.3. ⊆ = ∪ (1, 1)
1.3.4. ⊆ = ∩ (2, 2)
1.3.5. ⊆ ¬ ∥ (13, 20)
1.3.6. ⊆ ∥ ⊈ (1, 2)
1.3.7. ⊆ ∥ ≠ (3, 5)
1.3.8. ⊆ ∥ ∪ (7, 7)
1.3.9. ⊆ ∥ ∩ (2, 2)
1.3.10. ⊆ ⊈ ≠ (2, 3)
1.3.11. ⊆ ∪ ∩ (1, 1)
1.3.12. = ¬ ⊈ (1, 1)
1.3.13. ∦ ∥ ⊈ (1, 2)
1.3.14. ∦ ∥ ≠ (1, 2)
1.3.15. ¬ ∥ ∩ (1, 1)
1.4. Funktory czterech rodzajów (5, 5)
1.4.1. ⊆ ∦ ∥ ⊈ (1, 1)
1.4.2. ⊆ ¬ ∥ ∩ (1, 1)
1.4.3. ⊆ ∥ ∪ ∩ (3, 3)
II. Rachunek zdań (43, 91)
2.1. → (5, 24)
2.2. → ~ (13, 41)
2.3. → ∧ (8, 9)
2.4. → ∨ (1, 1)
2.5. ~ ∨ (1, 1)
2.6. ~ ⊻ (1, 1)
2.7. → ~ ∧ (3, 3)
2.8. → ~ ∨ (8, 8)
2.9. → ~ ⊻ (1, 1)
2.10. → ~ ∧ ∨ (1, 1)
2.11. ↔ ~ ∧ ∨ ⊻ (1, 1)
III. Rachunek zdań + sylogistyka (reguły mieszane) (37, 48)
3.1. ⊆ → (6, 8)
3.2. ⊆ ∧ (1, 1)
3.3. = → (1, 1)
3.4. Funktory co najmniej trzech rodzajów, bez ∪ i ∩ (19, 27)
3.5. Funktory co najmniej trzech rodzajów z ∪ lub ∩ (10, 11)
IV. Dowody niewprost (6, 13)
V. ω-reguła (1, 1)
VI. Paralogizmy (4, 5)
VII. Reguły specyficzne (30, 33)
R1.1.1.1 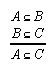 18, 20, 22, 22, 27, 34, 46, 57, 60, 84, 98, 99, 101, 110, 112, 116, 120, 120, 123, 125, 125, 126, 140, 140, 141, 141, 146, 147, 153, 158, 159, 208
18, 20, 22, 22, 27, 34, 46, 57, 60, 84, 98, 99, 101, 110, 112, 116, 120, 120, 123, 125, 125, 126, 140, 140, 141, 141, 146, 147, 153, 158, 159, 208
R1.1.1.2 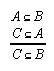 18, 18, 23, 27, 41, 42, 42, 64, 68, 71, 74, 74, 79, 95, 95, 104, 105, 107, 107, 123, 123, 135, 140, 148
18, 18, 23, 27, 41, 42, 42, 64, 68, 71, 74, 74, 79, 95, 95, 104, 105, 107, 107, 123, 123, 135, 140, 148
R1.1.1.3 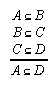 15, 21, 61, 72, 73, 102, 121, 148, 156
15, 21, 61, 72, 73, 102, 121, 148, 156
R1.1.1.4 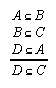 54, 155
54, 155
R1.1.1.5  32
32
R1.1.1.5a 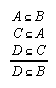 69
69
R1.1.1.6 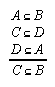 27, 27, 27, 27
27, 27, 27, 27
R1.1.1.7 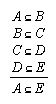 22, 62, 80, 99
22, 62, 80, 99
R1.1.1.8 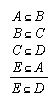 69, 97
69, 97
R1.1.1.9 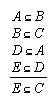 5
5
R1.1.1.10 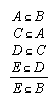 36
36
R1.1.1.11  102, 132
102, 132
R1.1.1.12 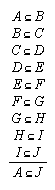 77
77
R1.1.2.1 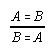 134
134
R1.1.2.2 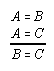 133
133
R1.1.2.3 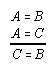 51
51
R1.1.2.4 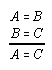 129, 301, 301
129, 301, 301
R1.1.2.5 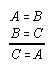 51
51
R1.1.2.6 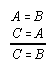 3, 43, 134, 217
3, 43, 134, 217
R1.1.2.7 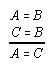 51
51
R1.1.2.8 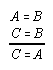 217
217
R1.1.2.9 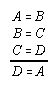 121
121
R1.1.2.10 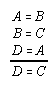 301
301
R1.1.2.11 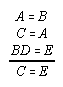 133
133
R1.1.3 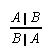 303
303
R1.2.1.1 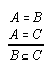 120
120
R1.2.1.2 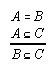 114
114
R1.2.1.3 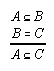 129, 217
129, 217
R1.2.1.4 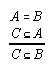 127, 133, 217
127, 133, 217
R1.2.1.5 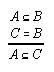 219
219
R1.2.1.6 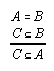 18, 18, 133, 148, 149, 217, 218
18, 18, 133, 148, 149, 217, 218
R1.2.1.7 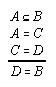 25
25
R1.2.1.8 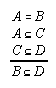 129
129
R1.2.1.9 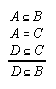 25
25
R1.2.1.10 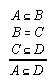 120
120
R1.2.1.11 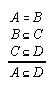 121
121
R1.2.1.12 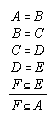 304
304
R1.2.2.1 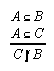 74
74
R1.2.2.2 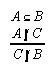 87
87
R1.2.2.3 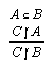 137, 137
137, 137
R1.2.3 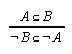 48
48
R1.2.4.1 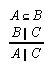 14, 29, 37, 39, 45, 48, 64, 91, 96, 99, 116, 125, 129, 140, 141, 150
14, 29, 37, 39, 45, 48, 64, 91, 96, 99, 116, 125, 129, 140, 141, 150
R1.2.4.2 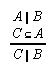 45, 100, 126, 137
45, 100, 126, 137
R1.2.4.3 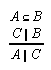 26, 26, 48, 50, 50, 67, 76, 76, 129, 152, 207, 207
26, 26, 48, 50, 50, 67, 76, 76, 129, 152, 207, 207
R1.2.4.4 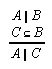 33, 53, 53, 92, 144, 156
33, 53, 53, 92, 144, 156
R1.2.4.5 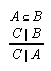 14, 17, 18, 18, 26, 37, 53, 53, 53, 91, 96, 124, 125, 137, 144
14, 17, 18, 18, 26, 37, 53, 53, 53, 91, 96, 124, 125, 137, 144
R1.2.4.6 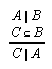 26, 26, 33, 145, 156
26, 26, 33, 145, 156
R1.2.4.7 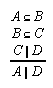 8, 65, 131
8, 65, 131
R1.2.4.8 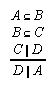 131
131
R1.2.4.9 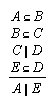 99
99
R1.2.4.10 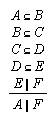 93
93
R1.2.5.1 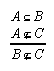 86
86
R1.2.5.2 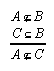 47, 82, 101
47, 82, 101
R1.2.5.3 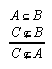 35
35
R1.2.6.1 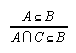 138
138
R1.2.6.2 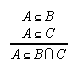 107
107
R1.2.6.3 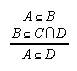 140
140
R1.2.6.4 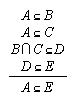 28
28
R1.2.6.5 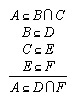 154
154
R1.2.6.6 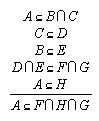 121
121
R1.2.7.1 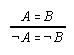 43
43
R1.2.7.2 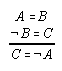 108
108
R1.2.7.3 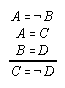 108
108
R1.2.8.1 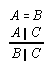 129, 301
129, 301
R1.2.8.2 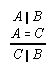 301
301
R1.2.8.3 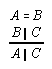 146
146
R1.2.8.4 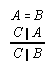 125, 127
125, 127
R1.2.9 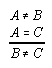 51
51
R1.2.10.1 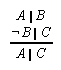 50, 51, 53, 53
50, 51, 53, 53
R1.2.10.2 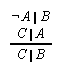 46, 46
46, 46
R1.2.10.3 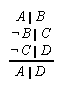 53, 93
53, 93
R1.3.1.1 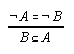 25
25
R1.3.1.2 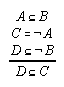 114
114
R1.3.2 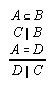 46
46
R1.3.3 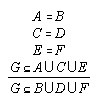 120
120
R1.3.4.1 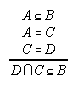 138
138
R1.3.4.2 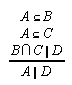 118
118
R1.3.5.1 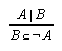 157
157
R1.3.5.2 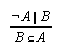 25, 121, 133
25, 121, 133
R1.3.5.3 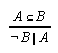 48, 53, 53, 53, 126, 128
48, 53, 53, 53, 126, 128
R1.3.5.4 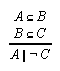 67
67
R1.3.5.5 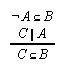 40
40
R1.3.5.6 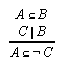 98
98
R1.3.5.7 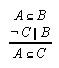 53
53
R1.3.5.8 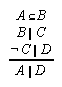 93
93
R1.3.5.9 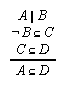 113
113
R1.3.5.10 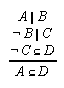 94
94
R1.3.5.11 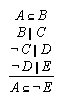 303
303
R1.3.5.12 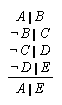 141
141
R1.3.5.13 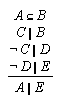 46
46
R1.3.6 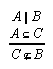 88, 306
88, 306
R1.3.7.1 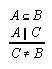 117
117
R1.3.7.2 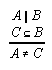 46, 302
46, 302
R1.3.7.3 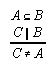 111, 142
111, 142
R1.3.8.1 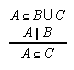 120
120
R1.3.8.2 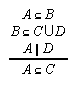 156
156
R1.3.8.3 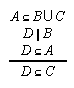 125
125
R1.3.8.4 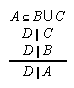 53
53
R1.3.8.5 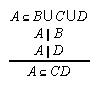 118
118
R1.3.8.6 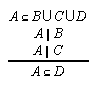 209
209
R1.3.8.7 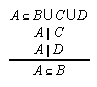 76
76
R1.3.9.1 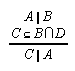 14
14
R1.3.9.2 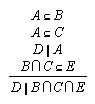 112
112
R1.3.10.1 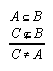 143
143
R1.3.10.2 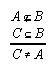 83, 85
83, 85
R1.3.11  118
118
R1.3.12 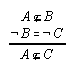 43
43
R1.3.13 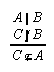 70, 88
70, 88
R1.3.14 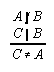 115, 156
115, 156
R1.3.15 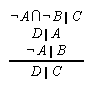 124
124
R1.4.1 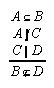 128
128
R1.4.2 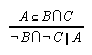 124
124
R1.4.3.1 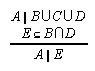 53
53
R1.4.3.2 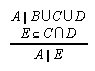 53
53
R1.4.3.3 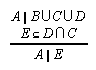 53
53
R2.1.1 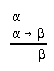 51, 53, 53, 53, 53, 53, 75, 202, 207, 207, 214
51, 53, 53, 53, 53, 53, 75, 202, 207, 207, 214
R2.1.2 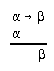 2, 51, 53, 66, 130, 130, 149, 153, 307
2, 51, 53, 66, 130, 130, 149, 153, 307
R2.1.3 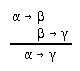 51, 215
51, 215
R2.1.4 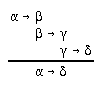 122
122
R2.1.5 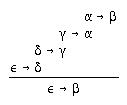 11
11
R2.2.1 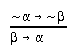 201, 206
201, 206
R2.2.2 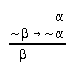 49, 205, 207
49, 205, 207
R2.2.3 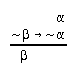 9
9
R2.2.4 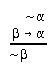 6, 53, 53, 207
6, 53, 53, 207
R2.2.5 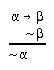 1, 1, 1, 14, 16, 32, 38, 52, 53, 53, 55, 63, 90, 215
1, 1, 1, 14, 16, 32, 38, 52, 53, 53, 55, 63, 90, 215
R2.2.6 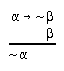 1, 16, 38, 38, 53, 53
1, 16, 38, 38, 53, 53
R2.2.7 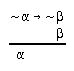 4, 12, 211
4, 12, 211
R2.2.8 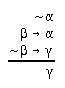 207
207
R2.2.9 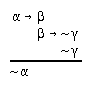 213
213
R2.2.10 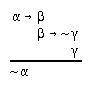 53, 204, 210
53, 204, 210
R2.2.11 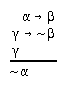 136
136
R2.2.12 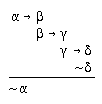 213
213
R2.2.13 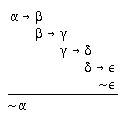 213
213
R2.3.1 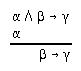 10
10
R2.3.2 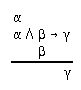 108
108
R2.3.3 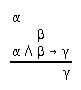 78
78
R2.3.4 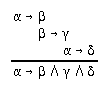 53
53
R2.3.5 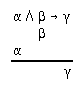 307
307
R2.3.6 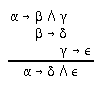 215
215
R2.3.7 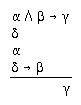 307
307
R2.3.8 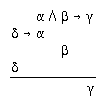 307, 307
307, 307
R2.4 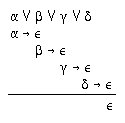 212
212
R2.5 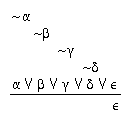 1
1
R2.6 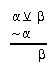 35
35
R2.7.1 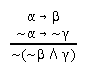 51
51
R2.7.2 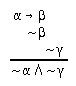 53
53
R2.7.3 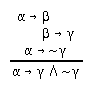 203
203
R2.8.1 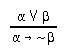 2
2
R2.8.2 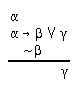 214
214
R2.8.3 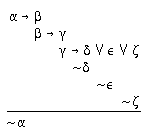 213
213
R2.8.4 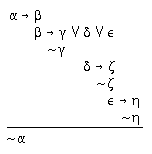 213
213
R2.8.5 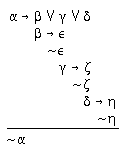 214
214
R2.8.6 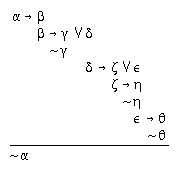 213
213
R2.8.7 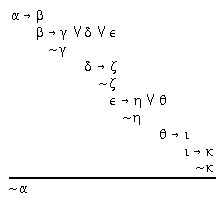 213
213
R2.8.8 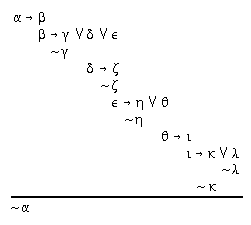 213
213
R2.9 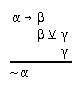 136
136
R2.10 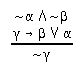 53
53
R2.11 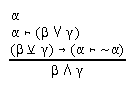 44
44
R3.1.1 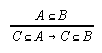 38, 56, 58
38, 56, 58
R3.1.2 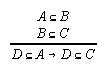 53
53
R3.1.3 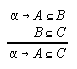 66
66
R3.1.4 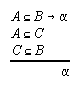 119
119
R3.1.5 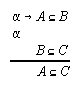 146
146
R3.1.6 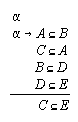 121
121
R3.2 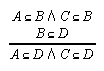 130
130
R3.3 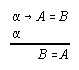 108
108
R3.4.1 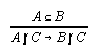 32
32
R3.4.2 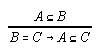 218
218
R3.4.3 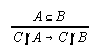 53
53
R3.4.4 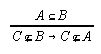 9
9
R3.4.5 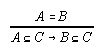 51
51
R3.4.6 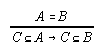 219, 220
219, 220
R3.4.7 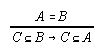 218, 219, 220, 220, 220
218, 219, 220, 220, 220
R3.4.8 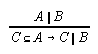 16, 38, 38, 216
16, 38, 38, 216
R3.4.9 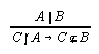 53
53
R3.4.10 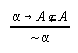 53
53
R3.4.11 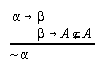 53
53
R3.4.12 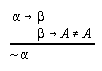 53
53
R3.4.13 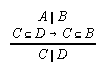 53
53
R3.4.14 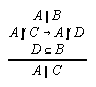 53
53
R3.4.15 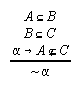 81
81
R3.4.16 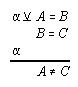 3
3
R3.4.17 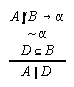 53
53
R3.4.18 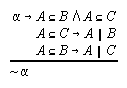 216
216
R3.4.19 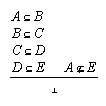 89
89
R3.5.1 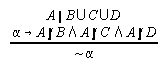 53
53
R3.5.2 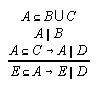 216
216
R3.5.3 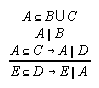 216
216
R3.5.4 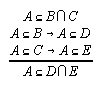 138, 138
138, 138
R3.5.5 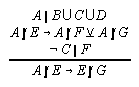 53
53
R3.5.6 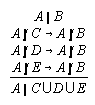 53
53
R3.5.7 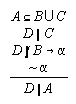 53
53
R3.5.8 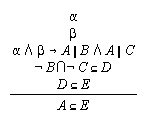 59
59
R3.5.9 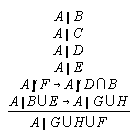 53
53
R3.5.10 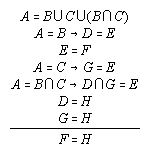 134
134
R4.1 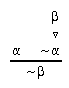 37, 99
37, 99
R4.2 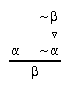 101
101
R4.3 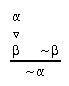 24, 43, 130, 130, 131, 307
24, 43, 130, 130, 131, 307
R4.4 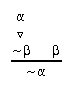 88, 129
88, 129
R4.5 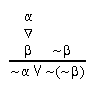 108
108
R4.6 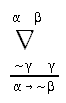 45
45
R5 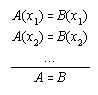 133
133
R6.1 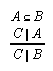 103, 103
103, 103
R6.2 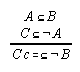 79
79
R6.3 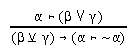 44
44
R6.4 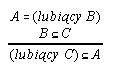 79
79
R7.1 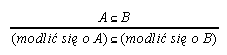 305
305
R7.2 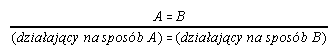 301, 301
301, 301
R7.3 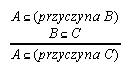 141
141
R7.4 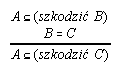 137
137
R7.5 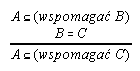 137
137
R7.6 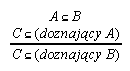 119
119
R7.7  31, 31, 31
31, 31, 31
R7.8 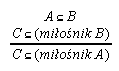 68
68
R7.9 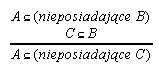 66
66
R7.10 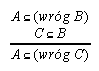 139
139
R7.11 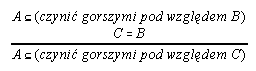 137
137
R7.12 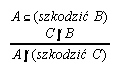 137
137
R7.13 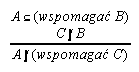 137
137
R7.14 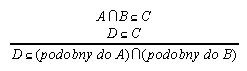 138
138
R7.15 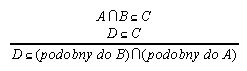 138
138
R7.16 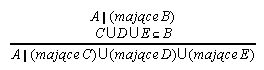 53
53
R7.17 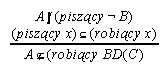 86
86
R7.18 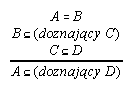 119
119
R7.19 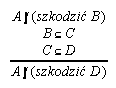 137
137
R7.20 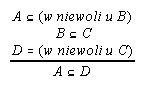 19
19
R7.21 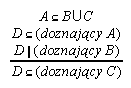 119
119
R7.22 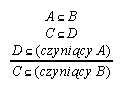 119
119
R7.23 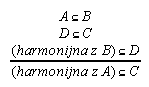 31
31
R7.24

140
R7.25
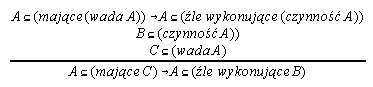
140
R7.26  40
40
R7.27 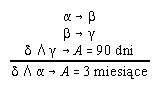 10
10
R7.28 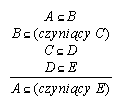 151
151
R7.29 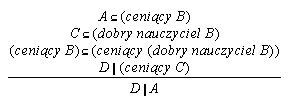 126
126
R7.30 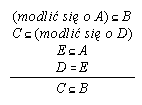 305
305
